Re: Re: Bewijs integraal van oneven functie is nul

Dit is een reactie op vraag 53896

Ik ben niet mee.
We doen dus:

de integraal= F(a) - F(-a)

We weten overigens dat F'= f en f is oneven.
Bijgevolg is F'(-a)= - F'(a)

Tot daar ben ik mee.

Maar ik begrijp niet dat afgeleide van een even functie juist oneven is, en de afgeleide van een oneven functie is even. En dat dat ook betekent : F(-a) = F(a).

Ik dacht dat bij een oneven functie: f'(-x) = - f'(x). En dat wil toch oneven zeggen niet?

Ik begrijp wel dat als heb dat F(-a) = F(a), het bewezen is.

vicky
Student universiteit België - dinsdag 15 januari 2008

Antwoord

dag Vicky,

Stel f is een even functie.
Dus f(-x) = f(x).

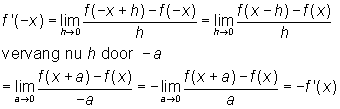
Dus f' is oneven.
Analoog kun je aantonen dat voor een oneven functie de afgeleide even is.
duidelijk zo?

Nog een aanvulling van medebeantwoorder kn:
integraal van -a naar 0 van f(x)dx
= - integraal van 0 naar a van f(-x)dx
= - integraal van 0 naar a van f(x)dx.
Zo eenvoudig kan het dus ook.

groet,

dinsdag 15 januari 2008

©2001-2024 WisFaq