Zwaartepunt van een halve parabool

Beschouwen we een 2de graadsparabool met als as de x-as en als top (0, 0). Beschouwen we van deze figuur enkel het gedeelte boven de x-as en over een afstand l op de x-as.

Wat is nu de x-coördinaat van het zwaartepunt van deze figuur?

---------------------------

Stel dat we op deze figuur (dus begrensd door de Y-as, de X-as en een vertikale lijn door x=l) nog een horizontale lijn trekken door het snijpunt van de vertikale lijn door x=l en de parabool.

Zo bekomen we een stukje parabool omschreven door een rechthoek als het ware.

Van het ene deel hebben we reeds de x-coördinaat van het zwaartepunt bepaalt, wat is nu de x-coördinaat van het zwaartepunt van het andere "complementaire" deel?

Jammer dat we hier geen figuren kunnen uploaden om onze vraag te verduidelijken...

Nathal
Student Hoger Onderwijs België - dinsdag 9 januari 2007

Antwoord

We kijken dus naar f(x)=√x met 0$<$x$<$l. Er geldt:



Voor l=10 hoort daar dan dit plaatje bij:



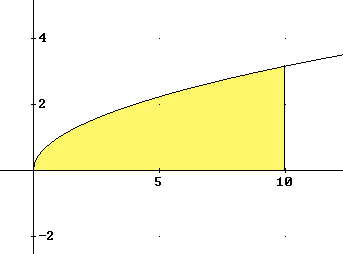
Je kunt dan de x_Z als volgt bepalen:



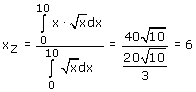
O... dat is sterk...

Nu staat er dat y_Z op dezelfde manier gaat, maar dan moet je natuurlijk niet de integraal nemen van y=0..√10 van x=y², want dan krijg je het zwaartepunt van het gebied links in plaats van rechts (onder en boven als je van links naar rechts kijkt).

Nee, je kan kijken naar het zwaartepunt van y=-x²+10 van 0 tot √10. Ga maar na! Uitwerken geeft:





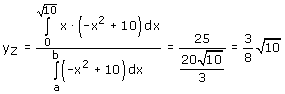
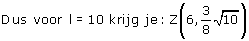
Volgens mij kan je hetzelfde doen voor l in plaats van 10. Toch?

zondag 14 januari 2007

©2001-2024 WisFaq