Berekenen van de standaardafwijking

Op dit moment zijn wij op school bezig met de normale verdeling en ik moet de standaardafwijking berekenen. Ik doe alle 5 de stappen en een simpel rekenvoorbeeld begrijp ik,maar als ik de opgave moet maken, krijg ik toch een andere uitkomst. Ook heb ik geprobeerd de voorbeeldopgave te maken en zelfs daar krijg ik de standaardafwijking niet. Ik zal hier de opgave geven waar ik op vastloop en ik kom dus ook niet verder in het boek:

gegeven is de frequentieverdeling van de scores behaald door 80 leerlingen bij een test. Bereken de standaardafwijking in een decimaal nauwkeurig

score frequentie
11-20 1
21-30 2
31-40 4
41-50 11
51-60 17
61-70 29
71-80 10
81-90 4
91-100 2

stap 1 ik neem de klassenmiddens en bereken het gemiddelde
(15.5*1)+(25.5*2)+(35.5*4)+(45.5*11)+(55.5*17)+(65.5*29)+(75.5*10)+(85.5*4)+(95.5*2)/80= 4789/80= 59.9 60=gemiddelde

stap 2 x - gemiddelde
15.5-60=-45, -35, -25, -15,-5,5,15,25,35

stap 3 d²=
2025,1225,625,225,25,25,225,625,1225 of
-2025,-1225,-625,-225,-25,25,225,625,1225
(ik heb het allebei geprobeerd)

stap 4 gemiddelde van de kwadraten:
6225/80=77.8

stap 5 standaardafwijking s=
Ö77,8=8,8

volgens het antwoordenboekje moet s zijn 14.9

Kunnen jullie me alsjeblieft verder helpen?

Debby
Leerling bovenbouw havo-vwo - zaterdag 16 april 2005

Antwoord

Je vergeet de 'kwadraatverschillen' te vermenigvuldigen met de frequentie. Je krijgt dan:



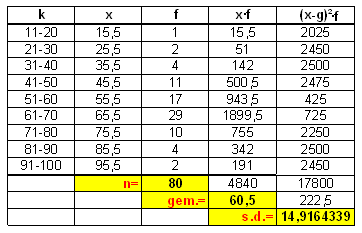
En dan klopt die 14,9 wel. En o ja... die minnen kunnen natuurlijk niet!

zaterdag 16 april 2005

©2001-2024 WisFaq