Een cirkeleigenschap bij de stelling van Pascal

Ik heb een vraag over de algemene stelling van Pascal. De algemene stelling gaat over kegelsneden, maar in het figuur van de door jullie zo vaak gegeven website gaat het om een cirkel. Nu weet ik dat een cirkel een speciaal geval van een kegelsnede is, maar kunnen jullie dit iets verder uitleggen? Verder zou ik ook nog willen weten waarom je de verschillende lijnstuken weg kan strepen door toepassing van de cirkeleigenschappen, want ik kan hier niet echt uitleg over vinden.

K
Leerling bovenbouw havo-vwo - dinsdag 15 maart 2005

Antwoord

Een deel van de figuur die op onderstaande website staat (en waarop je waarschijnlijk doelt met 'de door jullie zo vaak gegeven website') ziet er als onderstaand uit.

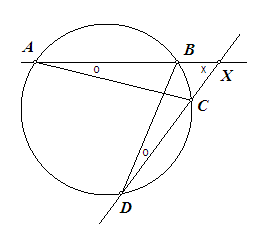
Bekijk nu eens de driehoeken AXC en DXB.
Daarin is A = ¹/₂bg(BC) ......omtrekshoek
en D = ¹/₂bg(BC) ......omtrekshoek
Beide driehoeken zijn dus gelijkvormig (waarom?).
Zodat:
AX / DX = XC / XB
en daaruit volgt dat AX · XB = CX · DX
Dit wordt, denk ik (;-), in het bewijs bedoeld met 'cirkeleigenschap'.
Zie je nu waarom je die (lengtes van de) lijnstukken in het bewijs tegen elkaar kan wegstrepen?

En voorts is het zo, dat als je de cirkel denkt in een vlak (en de lijnen liggen daar natuurlijk ook in) en dat vlak via parallelprojectie projecteert op een tweede vlak (niet evenwijdig met het eerste), dat dan de cirkel wordt afgebeeld op een ellips. Maar rechte lijnen worden daarbij nog steeds op rechte lijnen afgebeeld. En collineaire punten blijven natuurlijk collineaire punten.
De stelling van Pascal geldt dus ook voor ellipsen (in plaats van cirkels).

En dat geldt ook voor projectiemethoden waarbij een cirkel wordt afgebeeld op een parabool of op een hyperbool (en rechte lijnen weer op rechte lijnen).

Zie De Stelling van Pascal

donderdag 17 maart 2005

©2001-2024 WisFaq