Re: Hoogtelijnen in een gelijkbenige driehoek (analytisch)

Dit is een reactie op vraag 33969

Deze vraag heb ik eerder vandaag gesteld ik ben alleen er vergeten bij te zetten dat ik deze vraag geheel analytisch moet beantwoorden .
Hiervoor mijn excuses. Ik zou alleen wel heel graag willen weten hoe ik dit dus analytisch moet oplossen.
Alvast bedankt.

maarte
Leerling bovenbouw havo-vwo - zondag 13 februari 2005

Antwoord

Ok, met gebruik making van analytische methoden, en daaronder valt mijns inziens ook wat goniometrie (alleen iets weten over de rico van een lijn en over de cosinus).

Je mag in de analyische meetkunde een geschikt assenstelsel kiezen, en dat doe ik: AB is de x-as en ik kies A(-1,0), B(1,0), zodat O het midden is van AB.
Dan kiezen we voor C (dat op de y-as ligt): (0,c).

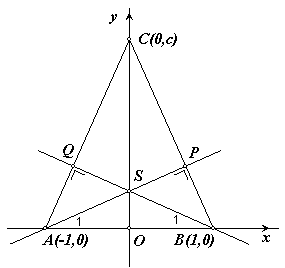
Ik ga ervan uit dat je weet dat het product van de rico's van twee lijnen die loodrecht op elkaar staan, gelijk is aan -1.

(a) Nu is
rico(BC) = -c en rico(AC) = c
zodat
rico(AP) = ¹/_c en rico(BQ) = -¹/_c
De hoeken A₁ en B₁ zijn dus gelijk. Waarom?
De cosinussen van die hoeken dus ook:
AP / 2 = BQ / 2 waaruit AP = BQ

Opmerking. Natuurlijk kan je eerst de coördinaten van P en Q berekenen (via vergelijkingen van lijnen) en dan met de afstandformule voor twee punten onderzoeken of AP = BQ.
Maar da's, vergeleken hiermee, heel wat werk.

(b) rico(AP) = ¹/_c
Dus (weet je waarom??) AP snijdt de y-as in het punt (0, ¹/_c)
rico(BQ) = -¹/_c
Dus BQ snijdt de y-as eveneens in het punt (0, ¹/_c)
Zodat AP en BQ elkaar snijden in hetzelfde punt van de y-as (en da's de loodlijn uit C op AB).

zondag 13 februari 2005

©2001-2024 WisFaq