Het centrum van de homothetie

Gegeven de punten: a(2,1), b(-1,3) en c(-2,-3) t.o.v. een orthonormale basis geijkt als (0,e1,e2) met lengteneenheid 0e = 1 cm.

Gevraagd:
(a) De coordinaten van "b", beeld van b door de orthogonale
spiegelmet de as A = ac(via berekening).

(b) Het beeld D te constueren door de homothetie h met factor (of verhouding) -1/3 en h(c) = a. Bepaal eerst het centrum van de homothetie h.

hl
Ouder - woensdag 22 december 2004

Antwoord

Allereerst maar eens een plaatje.

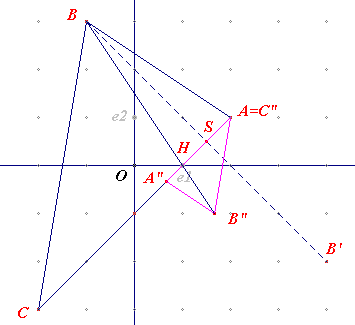
Ik gebruik parametervoorstellingen van lijnen.

(a)
AC: (x,y) = (2,1) + p (1,1)
Voor p = -¹/₂ geeft dit het punt S(1¹/₂, ¹/₂).
De loodlijn BB' op AC:
BB': (x,y) = (-1, 3) + q (1, -1)
Voor q = 0 vinden we het punt B.
Voor q = -2¹/₂ ligt ook hierop het punt S.
Voor q = -5 vinden we dan B' = (4, -2); immers q bepaalt een ijk op de lijn BB'.

(b)
factor = -¹/₃, maw. het centrum H van de homothetie ligt tussen A en C op de lijn AC, en wel zo, dat AH : HC = 1 : 3
A: p = 0
C: p = -4
Dus vinden we H voor p = -1; H = (1, 0).
Voor p = -1¹/₃ vinden we A" = (²/₃, -¹/₃).
Voor BH hebben we:
BH: (x, y) = (-1, 3) + r (2, -3)
B: r = 0
H: r = 1
zodat we B" vinden voor r = 1¹/₃; B" = (1²/₃, -1).

woensdag 22 december 2004

©2001-2024 WisFaq