Curven horizontaal optellen

Beste,
Bij een aanvullende studie werd ik plots geconfronteerd met het vak milieueconomie. Niet makkelijk voor iemand die uit een biologische richting komt… Om een bepaald vraagstuk op te lossen, moeten curven van bestrijdingskosten ‘horizontaal’ opgeteld worden. Hoe gaat dat ‘horizontaal optellen’ nou precies in zijn werk (ik had er nog nooit van gehoord)? De basisgegevens die bij dit vraagstuk horen zijn de volgende:

Stel twee vervuilingsbronnen a en b die een vergelijkbare emissie veroorzaken, waarbij :
MBKa = 12 – 2q en qa = 6
MBKb = 6 – q en qb = 6
De overheid wil deze emissie doen halveren en zal het instrument van de uniforme heffing toepassen.

Hopelijk kan u mij helpen zodat ik verder kan met het vervolg van het vraagstuk.
Vriendelijke groeten,
Tom

Tom VD
Student universiteit België - woensdag 4 augustus 2004

Antwoord

Beste Tom,

horizontale sommatie van 2 curven is niet echt wiskundig. Het is niet zo dat je de 2 functies op 1 of andere manier moet optellen. Je moet wel een grafische voorstelling maken. Ik heb hieronder al de 2 MBK-curves uitgetekend.


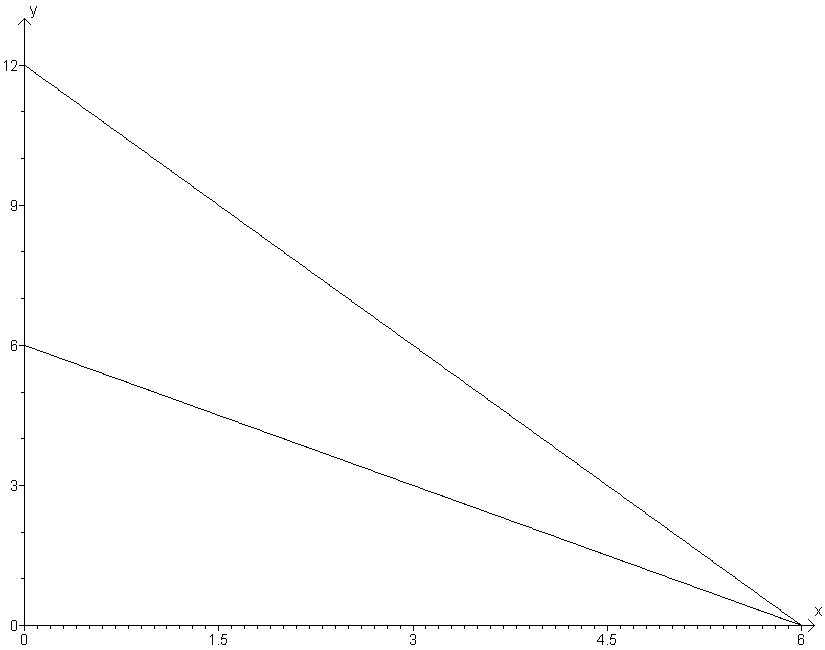
Je kan best zelf de 2 functies in een apart assenstelsel zetten, met daarnaast een derde assenstelsel voor de horizontale sommatie.

Voor de sommatie heb je 3 punten nodig. (n + 1 van het aantal functies, hier dus 3).
1) kijk naar de snijpunten met de y-as. Met de hoogste y-waarde (MBK-waarde in dit geval) begin je. Dat is 12, de overeenstemmende hoeveelheid is 0. De andere functie heeft geen MBK-waarde van 12 voor q 0, dus moeten we daar niet naar kijken. 0 + 0 = 0. Maak een nieuw assenstelsel en duid het punt (0,12) aan.

Als je de assenstelsels naast elkaar getekend hebt, kan je een lineaal nemen en die horizontaal leggen op y = 12. Elke rechte die je dan tegenkomt daar neem je de overeenstemmende x-waarde van, hier dus slechts 1 rechte. Nu doe je de lineaal naar y = 11, je hebt weer één rechte dus kijk je enkel naar die x-waarde bij y = 11. Nu, omdat je aan 1 rechte maar weinig op te tellen heeft, loopt de sommatie gewoon hetzelfde als MBKa in het begin. Dit wijzigt wanneer we 2 rechten hebben.

2) het breekpunt ligt waar MBKb met de y-as snijdt, dus op y = 6. qb = 0 en qa = 3 å = 3, dus het breekpunt ligt op (3,6)

3) het derde punt dat we nodig hebben, is steeds bij y = 0. De 2 overeenkomstige q waarden optellen (snijpunt met de x-as): 6 + 6 = 12, dus punt (12,0).

Je hebt nu 3 punten op je derde assenstelsel en die moet je met elkaar verbinden door 2 rechten (het is een rechte die breekt). We krijgen dan het volgende:


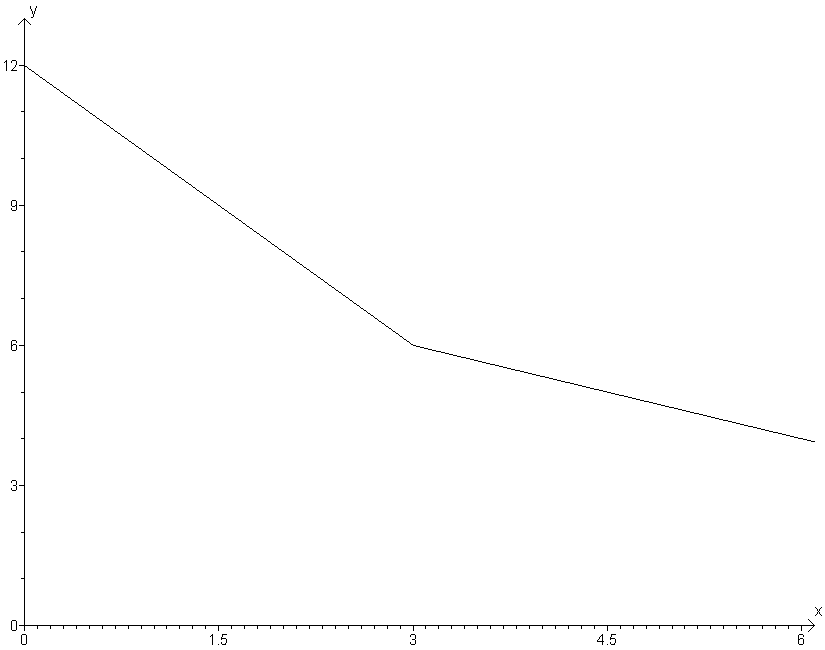
Het klinkt mss wat ingewikkeld, maar dat is het niet als je het een paar keer gedaan hebt. Het is eigenlijk een grafische methode die niet zo eenvoudig uit te leggen is.

Groetjes,

vrijdag 13 augustus 2004

©2001-2024 WisFaq