Bewijzen in een parallellogram

Gegeven: een parallellogram ABCD en de deellijn van hoek A is b. b snijdt BC in P en CD in Q.
Te bewijzen: de lengte van BA = de lengte van BP en de lengte van CP = de lengte van CQ.

babett
1ste graad ASO-TSO-BSO - maandag 2 februari 2004

Antwoord

Een plaatje zegt soms meer dan een tiental woorden, dus:

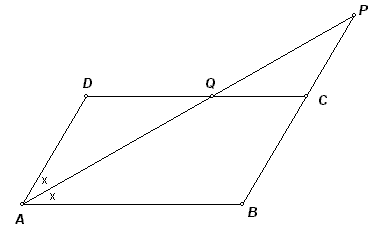
Let op de x-jes, die duiden op gelijke hoeken.
ABCD is een parallellogram. Wat weet je dan?
Er zijn meer hoeken waarin je zo'n x-je kan plaatsen... Doe dat eens!
Wellicht dat je nu zelf al het bewijs kunt geven. Zo niet, lees dan verder.

Je wilt bewijzen dat |AB|=|BP|.
AB en BP zijn zijden in driehoek ABP.
We redeneren terug.
ALS |AB|=|BP|, DAN is ABP een gelijkbenige driehoek!
Wat zijn in dat geval de basishoeken van die driehoek?
Hoe kan je bewijzen dat die hoeken gelijk zijn?
Tip: AD//BP en de lijn AP snijdt die evenwijdige lijnen.
Lukt het je nu?

En het tweede deel gaat eigenlijk op dezelfde manier.
ALS |CP|=|CQ|, DAN is driehoek PQC ...
De basishoeken zijn ...
Kan je ook dit bewijs verder afmaken?
Tip: gebruik nu dat AB//CD met als snijlijn weer AP.

Kan je ook bewijzen dat |AD|=|DQ|?
Succes!

(Enneh, maak je mailbox bij Hotmail regelmatig leeg!)

maandag 2 februari 2004

©2001-2024 WisFaq