Dubbelintegralen

op mijn (tweede zit) examen, moet ik een dubbelintegraal (òòf(x,y) ) oplossen door de integratiegrenzen van de twee veranderlijken om te wisselen. Ik veronderstel dat hiervoor wel een vaste werkwijze bestaat, maar in mijn cursus staat hiervan geen enkel voorbeeld uitgelegd. Ik hoopte dat jullie me misschien konden helpen door middel van een voorbeeldje... Alvast bedankt

Stépha
Student universiteit België - vrijdag 25 juli 2003

Antwoord

Ik denk dat je het omgooien van de integratievolgorde bedoelt. En dan is dit een interessant voorbeeld, denk ik...

Vraag:

Bereken

₀ò¹₀ò^Öy e^y/x dxdy

Oplossing:

Van het integrandum, beschouwd als functie in x, is niet onmiddellijk een primitieve functie te geven in termen van eenvoudige gekende functies. Als functie in y, is dat wel mogelijk. We gaan dus de integratievolgorde omwisselen en hopen dat, nadat y uit het integradum is "weggeintegreerd" het resultaat *wel* eenvoudig integreerbaar is (in x, dat op dat moment de enige veranderlijke is die nog overblijft).

Bekijk eerst het gebied in het (x,y)-vlak waarover de functie wordt geintegreerd. y, de onafhankelijke veranderlijke, varieert van 0 tot 1. Voor elke waarde van y varieert x van Öy tot 1, en die grenzen zijn afhankelijk van de waarde van y.



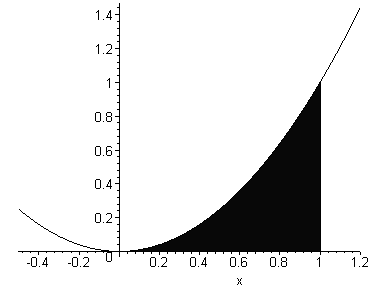
Laten we nu proberen de rollen van x en y om te wisselen: we maken van x de onafhankelijke variabele en van y de afhankelijke. In ons gebied blijkt x te varieren van 0 tot 1 en y van 0 tot x².

De integraal wordt nu (merk op dat er nu dydx staat ipv dxdy):

₀ò¹₀ò^x2 e^y/x dydx
= ₀ò¹ [x e^y/x]_y=0^y=x2 dx
= ₀ò¹ [xe^x-x] dx
= 1/2

Die laatste integraal is een "gewone" eendimensionale integraal die je in dit geval door partiele integratie kan berekenen.

zaterdag 26 juli 2003

©2001-2024 WisFaq