WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

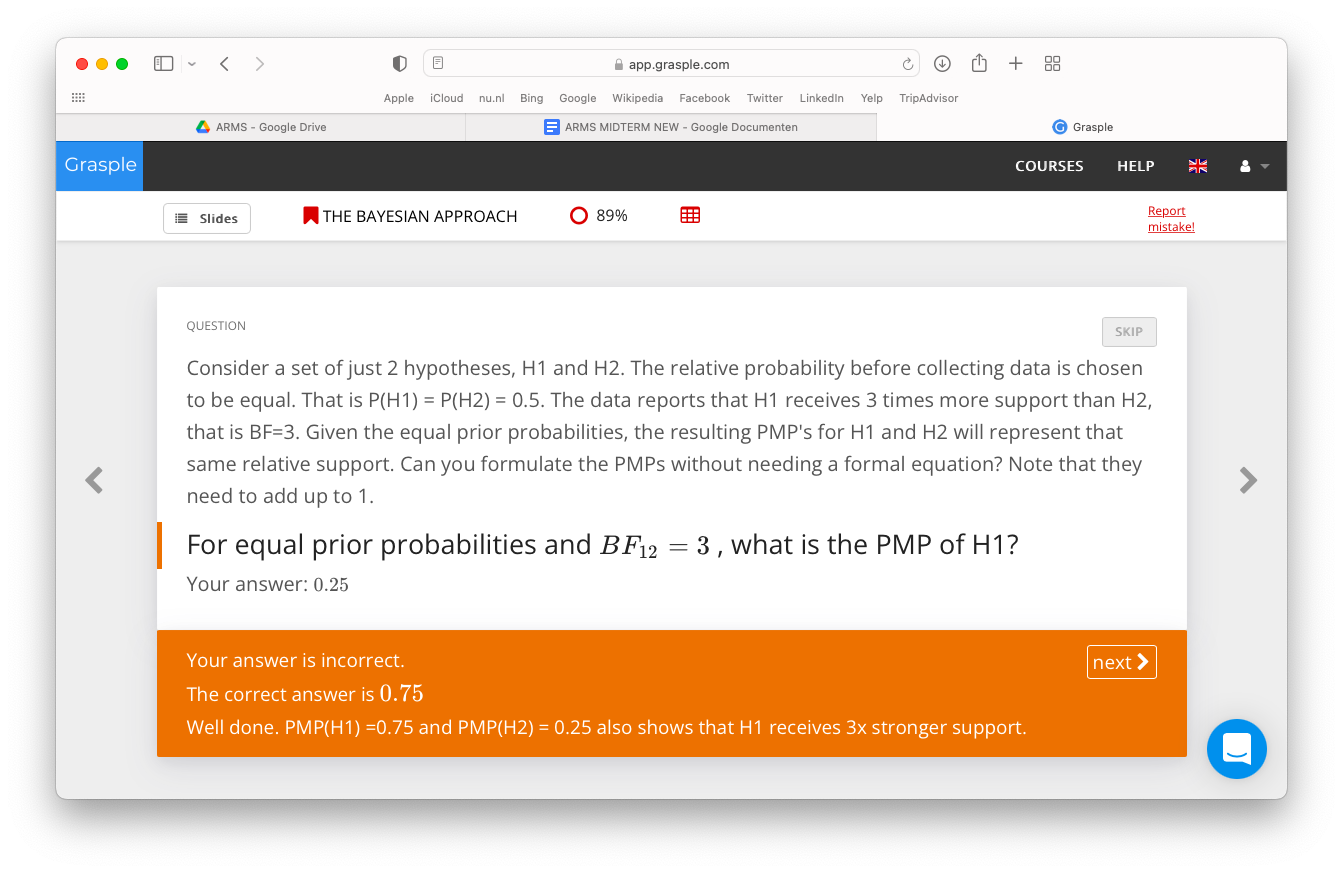
A-priori-kans (prior model propabilities)

Vertaling van de vraag:
Stel je hebt 2 hypothesen (H1 en H2). De relatieve waarschijnlijkheid vóór het verzamelen van de data is gelijk, namelijk P(H1) = P(H2) = 0.5. De data rapporteert dat H1 3 keer meer steun ontvangt dan H2, namelijk BF = 3. Doordat de prior probabilities gelijk zijn, zullen de PMP's van H1 en H2 die hieruit volgen dezelfde steun hebben.
Wat zijn de PMPs zonder dat je een formule gebruikt. Het antwoord moet uitkomen op een 1 als je het bij elkaar optelt.

Ik begrijp dat 0.25 x 3 = 0.75 en 0.25 + 0;75 = 1. Maar ik vraag mij af hoe je op dit antwoord kan komen zonder een formule te gebruiken?
Saja
Student universiteit - dinsdag 29 november 2022

Antwoord

De vraagstelling is wat subtieler: de kansen vooraf zijn niet gelijk, ze zijn gelijk gekozen. En er staat niet dat je het zonder formule moet doen maar zonder "formele vergelijking".
De redenering waar men aan denkt is waarschijnlijk als volgt: aangezien we $H_1$ en $H_2$ in het begin gelijke kansen toedenken bestaat de enige echte informatie die we hebben uit de relatieve frequenties van $H_1$ en $H_2$, aangezien die gelijk zijn aan $\frac34$ en $\frac14$ moeten we onze mening over de kansen op die twee herzien tot die twee getallen.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 30 november 2022