WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Toegepaste differentiaalrekenen

Dit is een reactie op vraag 90252

Beste,
Ik begrijp soort van waar jij naartoe wilt maar ik snap niet zo goed de logica waarom er geen 2 onbekende mogen zijn (de breedte dat gelijk is aan de diameter van de 2 halve cirkels, wat ik de x genoemd heb en de lengte van de rechthoek met als onbekende Y?

Wat is heb gedaan het totale oppervlakte van het stadion $>$
40000 m²=y.(1/4x²π) , x of y uithalen en daarna het totale omtrek vervangt en afgeleid $\ge$ Omtrek= 2x+yπ
Of ben ik het ver aan het zoeken?
Steeve
Student universiteit België - maandag 20 juli 2020

Antwoord

Hallo Steeve,

Wanneer je de breedte van de rechthoek x noemt en de lengte y, volgens onderstaande figuur, dan is de omtrek $\pi$x+2y en niet andersom.

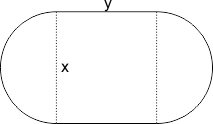
Hiermee kan je ook een formule opstellen voor de kosten van de afsluiting, dit wordt een functie van x en y. Omdat dit een functie is van twee variabelen, kan je niet 'de' afgeleide bepalen om een minimum te vinden. Er bestaat geen eenduidige afgeleide, wel partiële afgeleiden naar x en naar y. Daar heb je niet zoveel aan.

In werkelijkheid zijn er niet twee onafhankelijke variabelen. Wanneer je voor x een zekere waarde hebt gekozen, dan ligt daarmee de waarde van y vast. Immers, bij een zekere waarde van x is er maar één waarde van y waarbij de totale oppervlakte 40.000 m² is. Deze lengte y kan je dus uitdrukken in x, daarmee maak je de kosten afhankelijk van slechts één variabele x in plaats van afhankelijk van twee variabelen. Dan kan je wel via de afgeleide de waarde van x vinden waarvoor de kosten minimaal zijn.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 20 juli 2020

Re: Re: Re: Re: Toegepaste differentiaalrekenen