|
|
|
\require{AMSmath}



Re: Re: Steekproef bepalen
Beste Jadex, bedankt voor je reactie,
Ik heb nog twee vragen over dit onderwerp namelijk:
is er een bron voor deze formule waar ik naar kan parafraseren en, waar is de P waarde van 50 nu op gebaseerd indien ik zonder correctie de gewenste respons zou willen bepalen?
Ik neem aan dat dit een variabele moet zijn anders zou ik voor elke steekproef dezelfde waarde krijgen.
Graag je reactie.
Grt. Maurice
Mauric
Student hbo - zondag 26 mei 2019
Antwoord
Hallo Maurice,
Wanneer je aan een aantal mensen een ja/nee-vraag stelt, dan is het aantal keer dat met 'ja' wordt geantwoord binomiaal verdeeld (ervan uitgaande dat een zekere proportie p mensen 'ja' zou antwoorden en de rest 'nee'). Wanneer je zo'n steekproef vaak zou herhalen, dan merk je dat de gevonden steekproefproporties 'ja-zeggers' normaal verdeeld zijn, het gemiddelde hiervan is gelijk aan de populatieproportie. Voor de standaardafwijking $\sigma$ geldt:
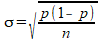
In het antwoord waarnaar je verwijst, vind je hoe je vanuit een gemiddelde waarde en een standaardafwijking een betrouwbaarheidsinterval berekent. Uitleg hierover vind je in elk statistiekboek over dit onderwerp, of bijvoorbeeld op Wikipedia: betrouwbaarheidsinterval.
Nu wil je van tevoren berekenen wat je steekproefomvang zou moeten zijn, zodanig dat je betrouwbaarheidsinterval klein genoeg is. Het probleem hierbij is dat de breedte van je betrouwbaarheidsinterval afhangt van de standaardafwijking $\sigma$, en deze hangt weer af van de proportie p. Maar je kent de waarde van p nog niet, hiervoor moet je eerst je steekproef uitvoeren.
Om toch verder te kunnen, kies je de waarde van p waarbij de standaardafwijking maximaal wordt. Dit is bij p=0,5 (ofwel 50%). Ga voor jezelf na dat $\sigma$ inderdaad maximaal wordt voor p=0,5. Je vindt dan de grootst mogelijke waarde van $\sigma$, dus de grootst mogelijke breedte van het betrouwbaarheidsinterval.
Wanneer je steekproef bij deze keuze groot genoeg is (d.w.z.: het betrouwbaarheidsinterval is klein genoeg), dan zal je steekproef zeker groot genoeg zijn wanneer achteraf blijkt dat p een andere waarde heeft dan p=0,5. De keuze voor p=0,5 kan je dus zien als uitgaan van een 'worst case scenario'.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 8 juni 2019
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 87942
Dit is een reactie op vraag 87942