WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Normale verdeling: rekenen met de normale verdeling

Dag Wisfaq

Zou u het volgende vraag voor me oplossen.

Een fabrikant van kogellagers wil kogeltjes bestellen met een diameter van 8mm en een tolerantie van 0,025mm. Hij verwacht dat 95% van alle kogeltjes aan de norm voldoen.

1) Wat is de kans dat een lukraak gekozen kogeltje voldoet aan de gestelde norm als de stadaardafwijking 0,02mm bedraagt?

2) Zal de fabrikant van kogellagers zijn bestelling plaatsen als de staandaardafwijking gehaalveerd is?

Ik weet niet welke moet ik nemen voor de formule normalCdf.
Zou ik mogen vragen om de uitleg van het dit vraag.

Alvast bedankt.
slm af
Overige TSO-BSO - woensdag 29 november 2017

Antwoord

Maak bij opgaven over de normaalverdeling steeds eerst een schets. Deze ziet er altijd zo uit:

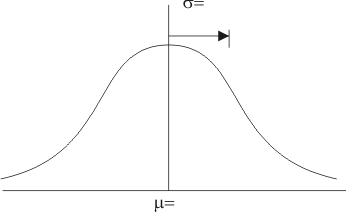
Bedenk welke grootheid langs de as gaat, en noteer de gegevens in de schets. In dit geval:
Het gaat over de diameter van kogeltjes
De gemiddelde waarde ($\mu$) is 8
De standaardafwijking ($\sigma$) is 0,02
We krijgen dus:

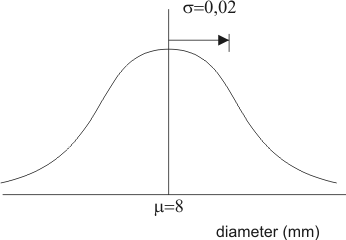
De standaardafwijking is de horizontale afstand tussen het hoogste punt van de curve en een buigpunt. Zelf vind ik het handig om dit met het pijltje aan te geven, dan kan je alvast schatten welke waarden je langs de horizontale as kunt verwachten. Je kunt dan zien of uitkomsten kunnen kloppen.

We zoeken ook twee grenzen die een gebied afbakenen. In dit geval gaat het om een tolerantie in diameter van 0,025 mm. De 'goede' kogeltjes hebben dus een diameter tussen 8-0,025=7,975 mm en 8+0,025=8,025 mm. Geef ook deze grenzen in de figuur aan, en kleur/arceer het gebied waarover de opgave gaat:

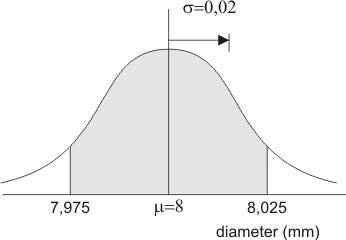
Dit arceren helpt om vergissingen te voorkomen. Wanneer bijvoorbeeld de vraag zou gaan over 'foute' kogeltjes, dan had je het gebied buiten deze grenzen moeten kleuren.

De gevraagde kans wordt gegeven door de oppervlakte van het gekleurde gebied. De vier benodigde gegevens zijn bekend:
linker grens = 7,975
rechter grens = 8,025
$\mu$ = 8
$\sigma$ = 0,02
Nu wordt het tijd om je rekenmachine te pakken en deze oppervlakte met behulp van de functie NormalCdf te berekenen. Overtuig je ervan dat je deze vier gegevens op de juiste manier invoert. Bij nieuwere rekenmachines kan dit via een menu, dan is er geen misverstand over de juiste volgorde. Bij iets oudere TI-rekenmachines moet je de gegevens in bovengenoemde volgorde invoeren:

NormalCdf(7.975,8.025,8,0.02)

Ik meen me te herinneren dat de volgorde bij oudere Casio rekenmachines is: linker grens, rechter grens, $\sigma$, $\mu$.

Ik vind een oppervlakte (en dus een kans) van 0,789 ofwel 78,9%. Dit is tevens het percentage kogeltjes dat aan de norm voldoet.

Vraag 2 pak je op dezelfde manier aan: uiteraard kies je een nieuwe waarde voor de standaardafwijking.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 29 november 2017