WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Extremumvraagstuk vuurpijl

Dit is een reactie op vraag 84484

Maar x_p = y_p = 50m en trekt die van elkaar is 0. Enkel die y coördinaten van die vuurpijl en boom zijn anders
Suys S
Student Hoger Onderwijs België - vrijdag 26 mei 2017

Antwoord

Hallo Suys,

Waarom denk je dat x_P = y_P = 50 m? Wanneer je zorgvuldig een schets maakt, zie je dat dit onjuist is:

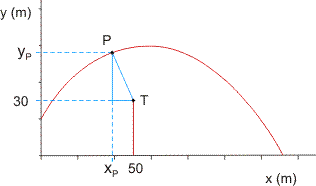
Wellicht bedoel je x_P = x_T, maar de afstand van top van de boom naar de vuurpijl hoeft niet minimaal te zijn wanneer de vuurpijl recht boven de boom is.

In de figuur zie je dat de horizontale zijde van het driehoekje gelijk is aan (50-x_P), de verticale zijde is (y_P-30).
Vul voor y_P jouw formule in, en stel dan met Pythagoras een formule op voor de lengte PT. Vervolgens kan je met behulp van de afgeleide de minimale waarde van PT vinden.

Tip: met Pythagoras kan je vrij gemakkelijk een formule opstellen voor (PT)². Je kunt ook de afgeleide van deze formule gebruiken. Immers, wanneer (PT)² minimaal is, dan is PT ook minimaal. De afgeleide van de formule voor (PT)² is eenvoudiger.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 26 mei 2017

Re: Re: Re: Re: Extremumvraagstuk vuurpijl