WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verzameling toppen

Beste,

Voor elke waarde van a wordt een Oxy-vlak een kromme gegeven met vergelijking y=x³+ax². Elke kromme heeft 2 toppen, deze toppen vormen weer een kromme. Nu is de vraag om de vergelijking voor deze kromme af te leiden.

Ik heb werkelijk geen idee hoe ik dit moet aanpakken..
Zou u me op weg kunnen helpen?

Alvast bedankt!
Atena
Leerling bovenbouw havo-vwo - dinsdag 9 februari 2016

Antwoord

Hallo Atena,

Hieronder zie je een schets met krommen voor twee verschillende waarden van a (zwarte krommen) en de nieuwe rode kromme die door de zwarte toppen gaat:

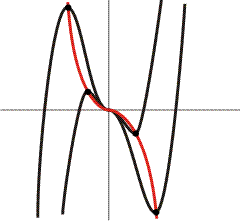
In elke zwarte stip (snijpunt van een zwarte top met de rode kromme) geldt:

y = x³+ax²

Want de stippen liggen op de grafiek van y. Maar in de zwarte stippen geldt ook:

y'(x) = 0
dus:
3x²+2ax=0

Want bij een top van een zwarte curve is de helling (dus: de afgeleide) gelijk aan nul.

Schrijf de tweede vergelijking nu in deze vorm:

a = .......

Dit kan je weer invullen in de eerste vergelijking. Je vindt dan een nieuwe vergelijking die de rode kromme beschrijft: deze voldoet aan beide voorwaarden, dat wil zeggen: deze snijdt de zwarte krommen op de plaats waar de afgeleide nul is.

Lukt het hiermee?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 februari 2016