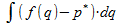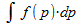WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integreren

Ik heb wat problemen met het opstellen van integralen. Dit is nogal vrij theoretisch en ik vind geen goede oplossingen voor mijn vraag op het internet.
Vraag: Neem nu een grafiek met een vraagcurve en een aanbodcurve. Indien ik het consumentensurplus zou willen berekenen hoe moet ik dan de integraal opstellen. Ik weet natuurlijk welke integraal ik nodig heb maar het gaat hem om de opstelling van de integraal.
Het consumentensurplus is de bepaalde integraal tussen 0 en q0 van de inverse vraagfunctie.
Mijn vraag gaat er eigenlijk over stel nu dat ik de integraal wil lezen vanuit de andere as van de grafiek hoe dat ik dan die integraal moet opstellen? (Was een vraag op mijn examen en ik ben het antwoord schuldig moeten blijven).
Integreren

Mike
Student universiteit België - dinsdag 10 maart 2015

Antwoord

Hallo Mike,

Je stelt wel een heel algemene vraag, ik weet niet precies waar jouw moeilijkheden liggen. In het algemeen kan je met een integraal de oppervlakte berekenen onder de grafiek van een functie.

Op wikipedia vind ik de volgende figuur waarin de oppervlakte van het oranje gebied het consumentensurplus weergeeft:

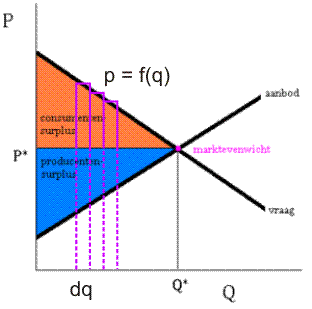
Kennelijk wil je deze oppervlakte met behulp van een integraal berekenen. Bij het integreren verdeel je zo'n oppervlakte in smalle staafjes. De hoogte van elk staafje wordt gegeven door de functiewaarde, hier dus:

Hoogte staafje = p-p^* = f(q)-p^*

f(q) is de formule die de waarde van p bepaalt, uitgaande van een waarde van q.

De breedte van de staafjes is dq. De oppervlakte van elk staafje is dan:

Oppervlakte staafje = hoogte × breedte = (f(q)-p^*)×dq

Hoe smaller de staafjes worden, hoe beter de oppervlakte van de staafjes de werkelijke oppervlakte van het oranje gebied weergeven. Het integreren komt er nu op neer dat de oppervlaktes van de staafjes worden opgeteld, waarbij de breedte dq van de staafjes naar oneindig klein gaat. We noteren dit als:

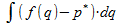
Nu vraag je hoe het zit wanneer je de integraal "wil lezen vanuit de andere as". Ik vermoed dat je hiermee bedoelt: p is niet bekend als functie van q, maar q is bekend als functie van p:

q = f(p)

In dat geval kunnen we de oranje oppervlakte berekenen met behulp van horizontale staafjes, zie de linker figuur hieronder.

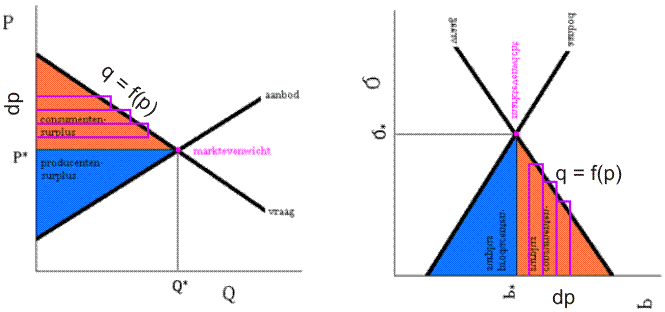
De "dikte" van de staafjes is nu dp, de lengte van de staafjes is f(p). De oppervlakte van zo'n staafje is dan:

Oppervlakte staafje = f(p)×dp

Het optellen van deze oppervlaktes gaat dan volgens deze integraal:

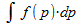
In de wiskunde is het gebruikelijk om de onafhankelijke variabele horizontaal uit te zetten en de afhankelijke variabele horizontaal. Omdat we p in de formule kunnen invullen (onafhankelijke variabele) en daarmee q kunnen berekenen (afhankelijke variabele), zouden we de assen moeten verwisselen. Dit heb ik in de rechter figuur gedaan. Je ziet dat we dan weer de 'gewone' verticale staafjes krijgen die de oppervlakte onder de grafiek weergeven.

Hopelijk helpt dit je verder.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 22 maart 2015