WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Extremumproblemen

Beste,

Ik heb morgen een test van extremumproblemen, maar ik snap er echt niks van! Ik ben niet de beste van de klas in wiskunde en kan dus vaak niet volgen. Ik wou een oefening maken, maar ik snap ze niet.

Opdracht
Lars krijgt 17m draad en moet hiermee een rechthoekig campingplaatsje afspannen, waarbij 1 zijde langs de rivier ligt (hier is geen afspanning nodig).
Bij welke afmetingen verkrijgt hij de grootst mogelijke oppervlakte?
Hoe groot is de oppervlakte dan?
Eerst doe ik dus: A=l×b dan is 17=l×b en dan zit ik vast. Heeft u misschien tips ofzo? Want ik ga gegarandeerd deze test verpesten.
M.v.g.
imani
2de graad ASO - maandag 20 oktober 2014

Antwoord

Het principe van veel van dit soort opgaven is om de maximale oppervlakte te vinden bij een gegeven omtrek of de maximale inhoud bij een gegeven oppervlakte en alle andere varianten die je maar kan bedenken.

Hier gaat het om een rechthoek met gegeven omtrek waarbij gevraagd wordt de maximale oppervlakte te berekenen. Druk de lengte uit in de breedte en druk de oppervlakte uit in de breedte en dan ben je er wel.

De kunst is dan om even een goede schets te maken en handige variabelen te kiezen en de oppervlakte uit te drukken in één variabele...

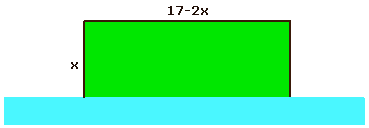
Bij een gegeven breedte $x$ is de lengte gelijk aan $17-2x$. De oppervlakte is dan gelijk aan $O(x)=x(17-2x)$. Dat is een tweedegraads formule. Bepaal vervolgens de $x$-waarde van de top... en dan ben je er wel uit.

Op 3. Optimaliseringsproblemen kan je een hele verzameling voorbeelden vinden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 20 oktober 2014