|
|
|
\require{AMSmath}



Sinusregel in koordenvierhoek
Stel koordenvierhoek ABCD. Diagonalen AC en BD.
Ik kom niet uit het volgende probleem: stel hoek(A)=90 graden. Het blijkt dat BD / sin(hoek(A)) = AC / sin(hoek(A)-hoek(CAD))
Herman
Ouder - zondag 19 januari 2014
Antwoord
Beste Herman,
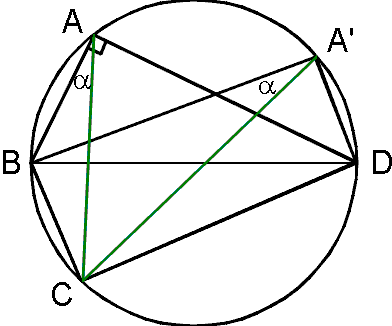
Uit $\angle$A=90° volgt: sin($\angle$A)=1
Verder zien we in de figuur:
$\angle$A-$\angle$CAD = $\angle$BAC, deze hoek noem ik $\alpha$
Jouw bewering wordt dan:
BD = AC/sin$\alpha$ ofwel:
AC = BD×sin$\alpha$
Dit kan niet waar zijn: in de figuur heb ik twee posities voor punt A gekozen (A en A'). Hoek $\alpha$ blijft constant (gelijke koorden hebben gelijke omtrekshoeken). BD en sin$\alpha$ zijn constant, maar duidelijk is dat AC en A'C niet even lang zijn, dit is in strijd met jouw uitspraak.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 19 januari 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










