|
|
|
\require{AMSmath}



Hoogte bepalen
In de database heb ik als een soort antwoord gevonden,maar daar kan ik niet verder mee.
Het gaat om een 10 meter hoge boom die omgeknakt is. De top van die boom raakt de grond op 6 meter van de stam.
Vraag: op welke hoogte is de knak. Nu besef ik dat ik het moet doen met Pythagoras en een variabele moet invoeren, maar ik kom daar niet verder mee. Ik weet ook dat beide zijden samen 10 zouden moet zijn.
Hartelijk dank, ben al het hele weekend daarmee bezig.
Corne
Leerling onderbouw vmbo-havo-vwo - zondag 9 september 2012
Antwoord
Ik neem aan dat je 't over Hoe bereken je de zijde van een driehoek? hebt. Je kunt ook reageren op vragen. Dat is wel zo handig.
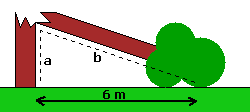
Op Hoe bereken je de zijde van een driehoek? staat een stelsel van twee vergelijkingen met twee onbekenden:
$
\left\{ \begin{array}{l}
a^2 + 6^2 = b^2 \\
a + b = 10 \\
\end{array} \right.
$
De eerste vergelijking komt van de stelling van Pythagoras. De tweede vergelijking van de lengte van de boom.
Zo'n stelsel van twee vergelijkingen met twee onbekenden zou je moeten kunnen oplossen. Maar misschien heb je dat (nog) niet gehad?
$
\begin{array}{l}
\left\{ \begin{array}{l}
a^2 + 6^2 = b^2 \\
a + b = 10 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
a^2 + 36 = b^2 \\
b = 10 - a \\
\end{array} \right. \\
Invullen: \\
a^2 + 36 = (10 - a)^2 \\
Oplossen! \\
\end{array}
$
Zou het dan lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 9 september 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










