WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verhouding inhouden

Hi,

De vraag dit zich stelt is de volgende:
- gegeven een bol met straal R en middelpunt O
- gegeven een tweede bol met straal R/2 en middelpunt O
- een vlak dat aan de tweede bol raakt

Nu is de vraag wat de verhouding is tussen de inhouden van de grote bol die door dat vlak worden afgesneden.

Dus wil ik het stuk boven onder het vlak gelegen berekenen, en zo vind ik automatisch het deel erboven (via inhoud van de totale bol), waaruit de verhouding volgt.

Om het stuk onder het vlak gelegen te berekenen, ga ik uit van de doorsnede in het vlak loodrecht op het beschouwde snijdende vlak, dit is dus een cirkel waarvan een stuk is weggeknipt.
Als oppervlakte hiervan vind ik nu:
2/3 * R² * + 3/4 * R²

dit werd berekend door de oppervlakte van de globale cirkel verminderd met het weggeknipte 'taartdeel' (hoek 120°) vermeerderd met de gelijkbenige driehoek met zijde R en ingesloten hoek 120°.

Nu zou ik door wenteling de inhoud willen berekenen van dit deel van de bol. Hoe doe ik dit precies?

Is er ook een alternatieve methode via een dubbelintegraal mogelijk om deze inhouden te berekenen???

Dank!
Koen
Student universiteit België - donderdag 9 januari 2003

Antwoord

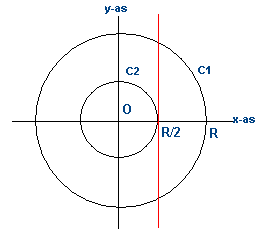
Als ik je vraag goed begrijp, dan is hierboven de bijbehorende doorsnede van de situatie geschetst.

Het gaat je om de verhouding van de inhouden van de grote bol, links en rechts van de rode lijn. toch?

Ik zou 't als volgt doen:

De inhoud van de gehele bol is (4/3) R³;
het volume van het gedeelte rechts van de rode lijn kun je berekenen m.b.v. integraalrekening. Het gaat dan natuurlijk om het omwentelingslichaam van cirkel C1, met ondergrens
R/2, en als bovengrens R
de vergelijking van C1: y=(R²-x²)
I_rechts= òy²dx
= ò(R²-x²)dx
= [R²x-¹/₃x³], met ondergrens R/2 en bovengrens R
= (R³-¹/₃R³-(¹/₂R³-¹/₃.(1/8)R³))
= R³(1-¹/₃-¹/₂+(1/24))
= R³.(5/24)

En dus is
I_links=(4/3) R³-I_rechts

En zo weet je ook:
I_links/I_rechts

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 januari 2003