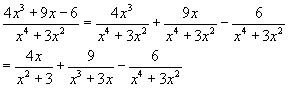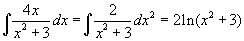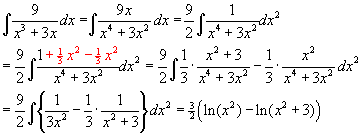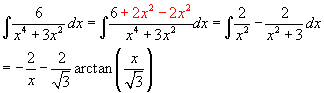WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integralen

Nog 2 integralen waar ik wat hulp bij nodig heb:
1)$\int{}$((4x³+9x-6)/(x⁴+3x²)) dx
2)$\int{}$((sin⁵(x))/(10-sin²(x))) dx

dank bij voorbaat;

Tom
3de graad ASO - dinsdag 29 januari 2008

Antwoord

integraal 1.
Eerst zou ik de breuk opsplitsen in delen:

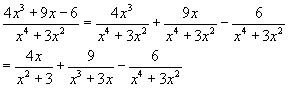
En daarna zou ik deel voor deel de primitieve bepalen, en uiteindelijk de 3 primitieves bij mekaar optellen.

deel 1:

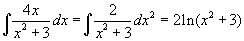
deel 2:

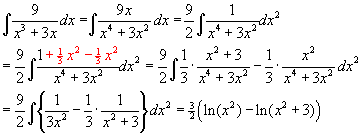
deel 3:

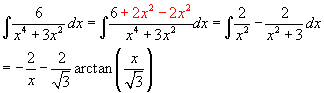
als je deze primitieves bij elkaar voegt (deel1 + deel2 - deel3) dan heb je de totale primitieve

De 2e integraal is zo mogelijk n$\int{}$g wat lastiger, maar is uiteindelijk op een zelfde soort probleem als het voorgaande terug te voeren:
in de teller verander je sin⁵x.dx in -sin⁴x.d(cosx)
en omdat sin²x+cos²x=1 wordt dit -(1-cos²x)².d(cosx)
de noemer, 10-sin²x, wordt zo 9+cos²x

Zo heb je het gehele probleem opgeschreven in termen van cosx.
Ofwel, je kunt de integraal nu gaan hanteren als:

$\int{}$-(1-y²)²/(9+y²) .dy

probeer het vanaf hier eens zelf verder.
Je antwoord kun je checken via
http://integrals.wolfram.com/index.jsp

groeten,

martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 29 januari 2008