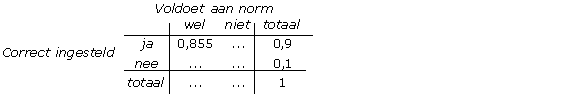WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Statistisch probleem

Bij een correcte instelling van een vulmachine blijkt 95 % van de afgeleverde verpakkingen aan een kwaliteitsnorm te voldoen (en 5 % dus niet). Volgens ervaring is de instelling van de vulmachine in 90 % van de gevallen in orde, in 10 % van de gevallen dus niet. Als de instelling niet in orde is, dan is de kans dat een afgeleverde verpakking niet aan de kwaliteitsnorm voldoet 0,8 (dus kans 0,2 dat nog wel aan de kwaliteitsnorm wordt voldaan).
a) Op een willekeurig moment wordt een verpakking gecontroleerd. Hoe groot is de kans dat deze aan de kwaliteitsnorm voldoet?
b) Op een willekeurig moment worden twee verpakkingen gecontroleerd. Hoe groot is de kans dat beide verpakkingen niet aan de norm voldoen? En hoe groot is op een wel en een niet?
c) Hoe groot is de kans dat de instelling van de vulmachine ontregeld is als beide gekeurde verpakkingen niet voldoen aan de norm?
d) Hoe groot is de kans dat de instelling van de vulmachine ontregeld is als van beide verpakkingen de ene wel en de andere niet aan de norm voldoet?

Nu ben ik na lang tobben tot het volgende gekomen;

a) (0,95*0,9) + (0,95*0,1*0,2) = 0,874 = 87,4% van de goede producten zijn goed
0,05*0,1*0,8 = 0,004 = 0,4% kans dat afgekeurde producten WEL goed zijn
Totaal = 87,4 + 0,4 = 87,8%
b) 100 – 87,8 = 12,2% kans op een afkeur product
c) 8%
d) 2%

Kan iemand mij vertellen of dit goed is?
Rogier
Student hbo - dinsdag 10 januari 2006

Antwoord

Je antwoorden zijn niet goed.
Ik heb de gegevens voor je in een boomdiagram gezet.
Wellicht heb je daar wat aan.

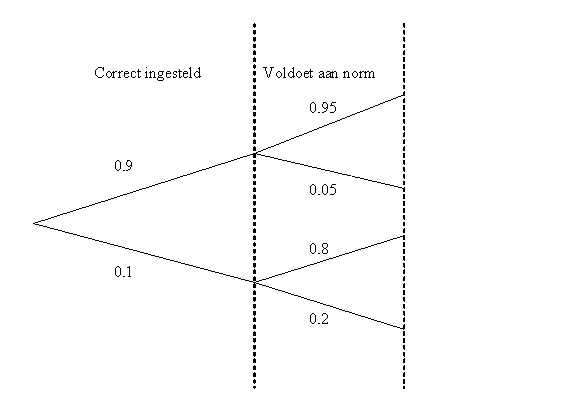
Uit het boomdiagram kan je vervolgens een kruistabel maken als:

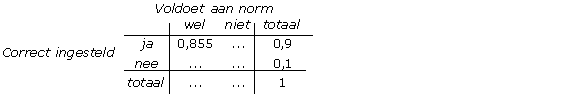
Succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 10 januari 2006