WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Booglengte van de parameterkromme

Dit is een reactie op vraag 39636

1. In mijn antwoordenboek staat: voor t van 0,25$\pi$ tot 0,75$\pi$. Als ik hem plot klopt dat ook, maar ik wil het zonder GRM doen.

2. Ik wist ook al dat ik moest integreren met die formule, maar het lukt me niet. Ik zal zeggen waar ik precies vast zit:

0,25$\pi \int{}$0,75$\pi$ √36cos²(2t)-64sin²(4t) dt =

0,25$\pi \int{}$0,75$\pi$ √18cos(4t)+18+32cos(8t)-32 dt

Doe ik het goed zo? Zo ja, da weet ik vanaf hier niet hoe ik verder moet. Zou het antwoord in stappen gegeven kunnen worden? Bij voorbaat dank!

Pastor
Leerling bovenbouw havo-vwo - zaterdag 2 juli 2005

Antwoord

Hallo,

Ja, dat klopt - ik had even over het hoofd gezien dat er niet zuiver sin(t) en cos(t) staan. Cos(4t) wordt volledig doorlopen als 4t natuurlijk een periode van 2$\pi$ doorloopt, dus t moet een interval van $\pi$/2 doorlopen. Je laat t in dit geval lopen van $\pi$/4 tot 3$\pi$/4.

In je integraal lijkt dat min-teken niet te kloppen, na kwadrateren is alles positief.
Het integreren is dan redelijk vervelend. Via sin(2x) = 2sin(x)cos(x) kan je nog wat vereenvoudigen en een cosinus onder de wortel uit halen. Je krijgt dan zoiets:

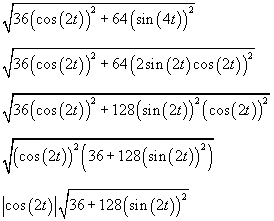
Erg eenvoudig wordt het echter nog steeds niet...

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 2 juli 2005