 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
||||||||||||||||||
|
\require{AMSmath}



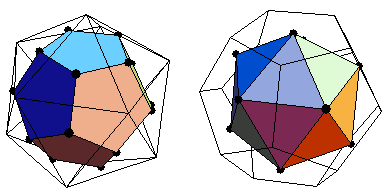
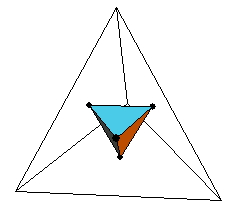
Dualiteit platonische lichamenBeste mensen, morgen moet ik mijn wiskunde po inleveren, en ik heb een vraagje over dualiteit. Ik heb het volgende schema gemaakt:t h o d iNu was de vraag hoe je die dualiteit kon zien in het schema. Heeft dat met orde van zijde en orde van hoekpunt te maken? Want de orde van zijde van een hexaeder is de orde van hoekpunt van een octaeder. En de orde van het hoekpunt van een hexaeder is de orde van een zijde van een octaeder. Zo ook bij het dodecaeder en een icosaeder. En als je twee tetraeders neemt ook. Antwoord
De dualiteit heeft inderdaad te maken met 'orde van zijde' en 'orde van hoekpunt'. Of zoals op http://www.georgehart.com/virtual-polyhedra/platonic-info.html staat: 'Observe that if {p,q} is a possible solid, then so is {q,p}.'.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| ||||||||||||||||||

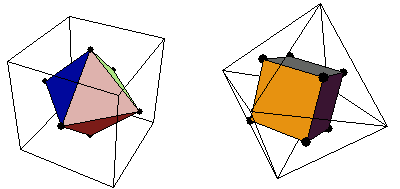


 Re: Dualiteit platonische lichamen
Re: Dualiteit platonische lichamen