WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Center of area van een kwart ellips

hoe bepaal je de 'center of area' van een kwart ellips?
De antwoorden zijn voor de y-coordinaat:4b/3pi en voor de x coordinaat: 4a/3pi. Maar ik weet niet hoe men daar aan komt, kunnen jullie mij daar bij helpen?
stepha
Student hbo - maandag 26 januari 2004

Antwoord

Het 'center of area' (ook wel 'zwaartepunt' genoemd, maar dat kan wel eens tot verwarring leiden!)van een oppervlakte vind je in het algemeen met behulp van het statisch moment.
We onderscheiden daarbij S_x en S_y.
S_x is het statisch moment tov de x-as en S_y het statisch moment tov de y-as.
In het meest eenvoudige geval (zoals met de kwart ellips) is de oppervlakte begrensd door de x-as, de y-as en een positieve functie f(x).
f(x) snijdt de x-as in (a,0) en de y-as in (0,b).
O is de oppervlakte van de figuur.
f^-1(x) is de inverse functie van f.
De formules voor de coördinaten van het zwaartepunt luiden dan:

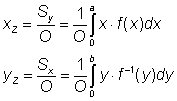
Ik hoop dat je hiermee geholpen bent
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 januari 2004