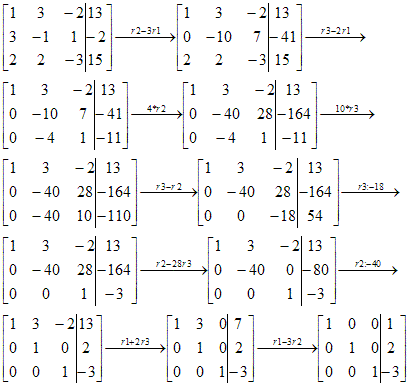|
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
||||||||||||||||||||||
|
\require{AMSmath}



3x3 stelselsWe hebben deze oefening in de klas ook gemaakt maar dan met substitutie nadien, maar mijn leerkracht zei ook dat je dat met matrixen verder kon uitwerken, wat we vorig schooljaar gezien hebben, het probleem is dat ik niet verder kan. AntwoordAls je het stelsel vergelijkingen in matrix-vorm omzet en daarmee verder rekent door de matrix “schoon te vegen”, dan blijven gewoon dezelfde regels gelden als bij het stelsel vergelijkingen.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| ||||||||||||||||||||||