In bijlage vindt u de 2 vragen.
(de 2 vragen lijken goed op elkaar)
Bij de eerste vraag heb ik dus een kubus gevormd met de bollen en de zijden gelijk gesteld aan a.
De diagonaal van het vierkant is √(2)*a en via de driehoek met schuine zijde de diagonaal van de kubus kun je ook deze diagonaal berekenen =√(3*(a)2)
via de cosinusregel zou je dan in de driehoek de hoek moeten kunnen berekenen door bv a gelijk te stellen aan een natuurlijk getal. Dan komt mijn cosinus groter dan 1 uit wat natuurlijk niet kan.
Zelfde probleem bij de 2de oefening.
ik bereken de diagonaal grondvlak= √(2)*5
dan maak ik opnieuw een driehoek met schuine zijde de schuine zijde piramide en hoek 90. diagonaal nu delen door 2. met pythagoras bereken je dan de schuine zijde =12.51.
Dan neem je de driehoek met onderste zijde de diagonaal vierkant en 2 schuine zijden 12.51. Via cosinusregel bereken je de hoek T en kom je ook voor cosinus een hoek uit groter dan 1
Hoe komt dit?max
27-4-2023
Hallo Max,
Je eerste vraag is al eerder beantwoord, zie Vraagstuk hoek berekenen ruimtefiguur. Laat het gerust weten als je nog problemen hebt met deze vraag, maar geef dan wel aan waar het probleem ligt.
Je aanpak voor vraag 2 is goed, alleen moet je de cosinusregel toepassen in driehoek TBC. De zijde tegenover hoek alfa is zijde BC=5, niet een diagonaal van het grondvlak van de piramide. Als je de cosinusregel netjes uitwerkt, kom je 'gewoon' op de gevraagde hoek:
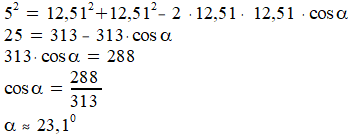
OK zo?
GHvD
28-4-2023
#97698 - Ruimtemeetkunde - 2de graad ASO