WisFaq!

Hoeken berekenen 6 hoekig puntdak

Een 6 hoekig puntdak (gelijkzijdig), De hoek tussen de spanten en het horizontale vlak is $\alpha $ b.v. 30°. De spanten zijn bijvoorbeeld 4 meter lang en 6 cm breed en 10 cm hoog. (niet echt relevant) tussen de uiteinden van twee spanten moet een vergelijkbare balk komen....wat lijkt....deze balk sluit bij beide uiteinden niet haaks aan op de spanten maar moet aan beide zijden over twee vlakken schuin afgezaagd worden!

De vraag wat zijn deze de hoeken? Bij voorkeur uitgedrukt in een afgeleide van hoek $\alpha $.

Wim
4-2-2023

Antwoord

Hallo Wim,

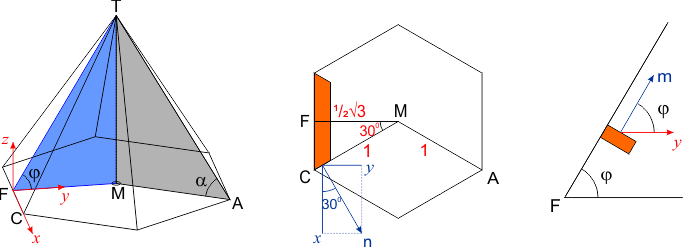
We hebben hier te maken met een dak in de vorm van een piramide met zeshoekig grondvlak, zie de figuur hieronder. De hoek tussen een spant (een ribbe van de piramide) en een horizontaal vlak (grondvlak) noemen we $\alpha$. Voor de berekeningen is het handiger om te rekenen met de hoek tussen een zijde en het grondvlak, in de figuur links aangegeven met $\varphi$.



We berekenen $\varphi$ als volgt:
De middelste figuur toont het bovenaanzicht van het grondvlak. In driehoek CMF is hoek M gelijk aan 30°. We stellen AM=CM=1, dan geldt FM=¹/₂√3. In driehoek AMT zien we: MT=tan(ALFA). In driehoek FMT geldt dan:



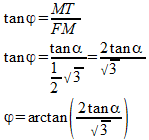
Voor de verdere berekeningen definieer ik eerst een assenstelsel met punt F als oorsprong, zie de figuur links. Het grondvlak ligt in het x-y-vlak, de z-as is omhoog.
In de twee rechter figuren is de bedoelde verbindingsbalk gekleurd weergegeven.
De oriëntatie van verschillende vlakken kunnen we aangeven met een vector die loodrecht op het bedoelde vlak staat (normaalvector). In de figuur rechts zien we dat de vector m loodrecht staat op de brede platte zijde van de verbindingsbalk. De hoek tussen m en de y-as is ook weer gelijk aan $\varphi$. In deze positie moet de kopse kant van de verbindingsbalk aansluiten op een spant in het verticale vlak CMT. In de middelste figuur zien we dan dat de normaalvector n op het kopse vlak van de verbindingsbalk in het x-y-vlak ligt en een hoek van 30° maakt met de positieve x-as. Coördinaten [x,y,z] van deze normaalvector kunnen zijn: [ √3 , 1 , 0 ].

Wanneer we nu de brede platte zijde van deze verbindingsbalk op een horizontale zaagtafel leggen, dan kantelt deze balk tegen de klok in onder een hoek van (90°-$\varphi$). Wiskundig is dit een rotatie rond de x-as. De normaalvector m komt dan verticaal te staan, dus in z-richting. De normaalvector n ondergaat diezelfde rotatie. De elementen van de geroteerde vecor n’ berekenen we door de vector n te vermenigvuldigen met een rotatiematrix:



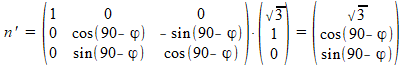
Omdat cos(90°–$\varphi$)=sin($\varphi$) en andersom, kunnen we ook schrijven:



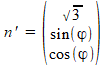
Zoals in de vaag al is gesteld, wordt de balk niet loodrecht op de lengterichting doorgezaagd om aan te sluiten op een spant. De hoek $\delta$ ten opzichte van loodrecht is gelijk aan de hoek van de projectie van n' in het x-y-vlak ten opzichte van de positieve x-as, zie de figuur hieronder.



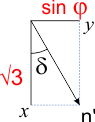
In deze figuur zien we:

tan($\delta$)=^{sin($\varphi$)}/_√3
$\delta$=arctan(^{sin($\varphi$)}/_√3)

De balk moet dus schuin worden doorgezaagd, onder bovengenoemde hoek ten opzichte van loodrecht.
De balk moet niet alleen schuin worden doorgezaagd, ook het zaagblad zelf moet schuin staan ten opzichte van het horizontale vlak van de zaagtafel. Om deze hoek $\gamma$ te berekenen, moeten we de hoek berekenen tussen de geroteerde normaalvector n' en het horizontale vlak, zie de figuur hieronder.



De z-coördinaat van n' is cos($\varphi$), de lengte van n' is 2. Hiermee berekenen we de hoek $\gamma$:

sin($\gamma$)=^{cos($\varphi$)}/₂
$\gamma$=arcsin(^{cos($\varphi$)}/₂)

Het zaagblad moet dus onder deze hoek schuin staan ten opzichte van verticaal om het kopse uiteinde van de verbindingsbalk te laten aansluiten op een spant.

Hopelijk heb ik geen rekenfout gemaakt, ik raad aan om eerst even op een proeflat te testen.

GHvD
8-2-2023