WisFaq!

Primitieven

Bereken de volgende integraal met de methode van de intervalmiddens. Bereken de integralen ook met de behulp van primitieven en vergelijk de resultaten.

In de oefening zijn er 2 vragen die ik niet kan oplossen

$
\eqalign{
& \int\limits_0^4 {4^x } dx\,\,\,{\text{voor}}\,\,\,n = 8 \cr
& \int\limits_2^7 {\frac{1}
{{x^2 - 1}}\,\,\,{\text{voor}}\,\,\,n = 10} \cr}
$

Zou u aub mij helpen met deze 2 vragen?
Met vriendelijke groeten

Riffat
12-6-2021

Antwoord

Eerst maar eens de primitieven. Beide integralen zijn standaard integralen.

Zo is de eerste primitieve functie F(x) = ¹/_ln(4)·4^x

De tweede primitieve functie is F(x) = -tanh^-1(x)
Het kan zijn dat je niet bekend bent met die laatste primitieve, dan is er ook nog een alternatief met breuksplitsen van de oorspronkelijke functie.

f(x) = 1/(x²-1) = 1/(x+1)(x-1) = (ga na) -0,5/(x+1) + 0,5/(x-1)
en dat primitiveren levert nu F(x) = -0,5·ln(x+1)+0,5·ln(x-1).
Als ik dat van 2 tot 7 laat lopen krijg ik als uitkomst 0,40547.

Nu voor de tweede opgave benadering met de intervalmiddens.



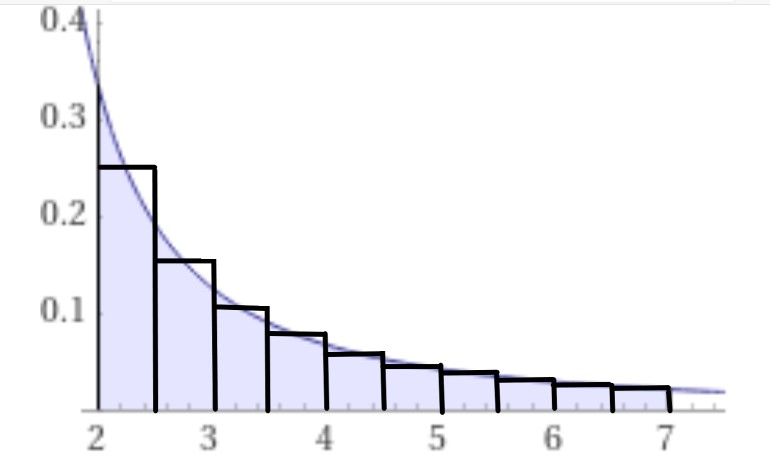
Je hebt 10 segmenten dus elk segment heeft breedte 0,5.
De oppervlakte van de eerste staaf is dan 0,5·f(2,25) = 0,123077. En zo doe je dat ook met de andere 9 staven en tel je alles op.

Met vriendelijke groet
JaDeX

jadex
12-6-2021