WisFaq!

Koekjes

In een fabriek worden koekjes gemaakt met een gemiddelde massa van 22 gram en een standaardafwijking van 4 gram. Een aantal koekjes wordt verpakt in een doos. Volgens de fabrikant is de gemiddelde massa van een koekje uit minstens 99% van de dozen minstens 20 gram. Hoeveel koekjes moet de fabrikant minstens in een doos steken?

R
11-5-2021

Antwoord

We beginnen op dezelfde wijze als bij je vorige vragen. Voor het gewicht X van koekjes (in gram) geldt:

$\mu$_X = 22
$\sigma$_X = 4

Voor de gemiddelde waarde X_gem van n koekjes in een doos geldt dan:

$\mu$_Xgem = 22
$\sigma$_Xgem = ⁴/_√n

De vraag is dan: Gegeven de normaal verdeelde variabele Xgem volgens N(22 ; $\sigma$_Xgem). Wat is de waarde van $\sigma$_Xgem zodat de kans op een waarneming van minstens 20 gelijk is aan 0,99?

Onderstaande figuur geeft deze vraag weer:



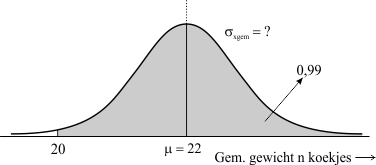
Lukt het om hiermee $\sigma$_Xgem te berekenen?

Wanneer je $\sigma$_Xgem weet, dan kan je n (=het aantal koekjes per doos) berekenen door onderstaande vergelijking op te lossen:

$\sigma$_Xgem = ⁴/_√n

Lukt het zo?

GHvD
11-5-2021