In dat geval moet aan twee voorwaarden worden voldaan om op tijd te komen:
- De trein moet uiterlijk 9:45 uur aankomen, anders mist Laura de bus;
- De bus moet uiterlijk 10:00 uur aankomen.
De overstaptijd is gemiddeld 4 minuten (van 9:41 uur tot 9:45 uur) met standaarddeviatie 3 minuten. Laura haalt de bus als de overstaptijd groter is dan nul. De vraag is dus:
Gegeven de normaal verdeelde variabele 'Overstaptijd' volgens N(4 , 3). Hoe groot is de kans op een waarneming groter dan nul? Onderstaande figuur geeft deze vraag weer:
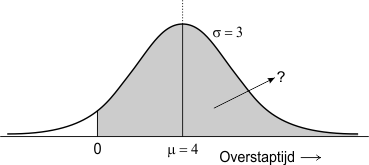
Ik vind: P(Laura haalt de bus)=0,909
Dan voorwaarde 2:
Toevallig heeft Laura nu ook gemiddeld 4 minuten tussen aankomsttijd bus en start acteerles, met dezelfde standaardafwijking van 3 minuten. Ook nu komt Laura op tijd bij een positieve waarneming. De berekening is toevallig dezelfde als hierboven, dus:
P(Bus arriveert op tijd)=0,909.
Voor de kans dat Laura op tijd komt, geldt:
P(Laura komt op tijd) = P(Laura haalt de bus en bus arriveert op tijd)
P(Laura komt op tijd) = P(Laura haalt de bus)·P(bus arriveert op tijd)
P(Laura komt op tijd) = 0,909·0,909 = 0,826
De kans dat Laura te laat komt, is dan 1-0,826 = 0,174
GHvD
10-5-2021