WisFaq!

Normale verdeling

Van een normaal verdeelde steekproef is het gemiddelde 100 gram en de standaarddeviatie 5 gram.

• Hoeveel procent van de waarnemingen ligt tussen de 87.3 en 103.8 gram.

Ik mag geen GR gebruiken. Extra oefeningen met alleen antwoord zonder uitleg

Antwoord is 77.12 procent.

Ik heb geen idee hoe ik hier aan zou moeten komen.

• Normale verdeling

Elijah Blue Vonk
26-2-2021

Antwoord

Bereken voor beide waarden de z-score. Zoek in de tabel de bijbehorende oppervlakte onder de grafiek en trek je conclusie!

$
\eqalign{
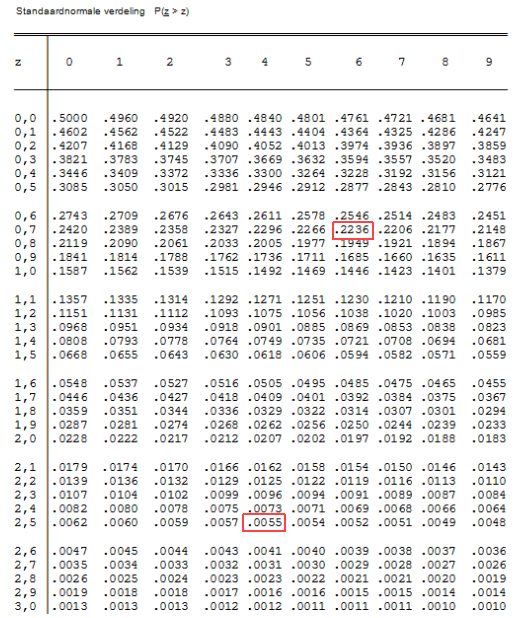
& z_1 = {{87,3 - 100} \over 5} = - 2.54 \cr
& \phi ( - 2.54) = {\rm{0}}{\rm{,0055}} \cr
& {\rm{z}}_{\rm{2}} {\rm{ = }}{{103,8 - 100} \over 5} = {\rm{0}}{\rm{,76}} \cr
& \phi ({\rm{0}}{\rm{,76) = 1 - 0}}{\rm{,2236 = 0}}{\rm{,7764}} \cr
& \phi ({\rm{0}}{\rm{,76) - }}\phi ( - 2.54) = 0,7709 \cr}
$



..en dan lukt het wel...

WvR
26-2-2021