Dag team WisFaq
Mijn vraag ging over de Rechte van Simson. Ik begrijp de stelling en het bewijs, maar zit vast bij volgende vraag:
"Toon aan dat de rechte van Simson van een punt P t.o.v. een driehoek ABC evenwijdig is met de rechte P'A waarbij P' het tweede snijpunt van PA' met de omgeschreven cirkel."
Ik heb het volgens mij wel juist geconstrueerd, maar ik weet niet precies hoe ik moet beginnen aan het bewijs.
Alvast bedankt!
Lotte van Brabant
26-12-2020
Dag Lotte,
Ik maakte ook een tekening.
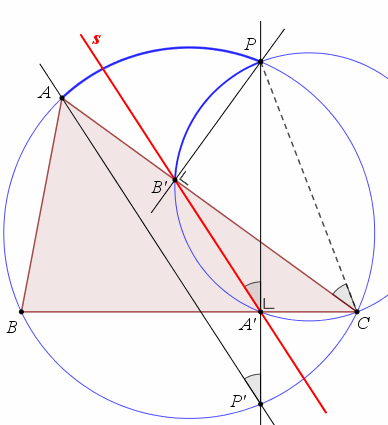
De punten A' en B' zijn de projecties van P op de zijden. En ik heb de cirkel getekend bij de koordenvierhoek PB'A'C. En in de figuur zijn ook enkele bogen en hoeken geaccentueerd.
Gebruik omtrekshoeken, eerst op de kleine cirkel, dan op de grote!! En daarmee moet het nu lukken!
Groet,
dk
27-12-2020
#91237 - Vlakkemeetkunde - 2de graad ASO
