Het gaat dan om twee aparte gebieden. Het deel van $x=0$ tot $x=1$ is een integraal van $e^x$ en het deel van $x=1$ tot $x=2$ is dan een integraal van $e^x-ln(x)$.
De rest is dan een kwestie van invullen en uitrekenen.

WvR
7-12-2020
Ik heb gegeven; y=ex, y=lnx, y=0, x=0 en x=2. Ik moet hiervan de opervlakte berekenen maar ik snap niet hoe. Wat moet ik doen met de y=0? Ik kan de oplossing doorsturen als plaatje. Ik snap niet hoe ze aan de bovengrens en ondergrens 2 en 1 komen.melike
7-12-2020
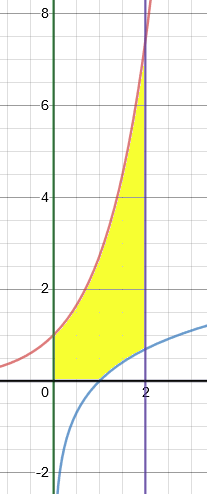
Als je de grafieken plot krijg je het volgende plaatje. Ik neem aan dat het gaat om de oppervlakte van het gele deel. Dat is het deel dat ingesloten wordt door de twee functies, $y=0$ en $x=0$ en $x=2$.
Het gaat dan om twee aparte gebieden. Het deel van $x=0$ tot $x=1$ is een integraal van $e^x$ en het deel van $x=1$ tot $x=2$ is dan een integraal van $e^x-ln(x)$.
De rest is dan een kwestie van invullen en uitrekenen.
WvR
7-12-2020
#91133 - Integreren - Student universiteit BelgiŽ