WisFaq!

Re: Re: Re: Re: Functieonderzoek

Ja, het is gelukt dankuwel. Voor verder onderzoek zou ik ook de afgeleide en de volgende afgeleide moeten berekenen voor f(x).

Ik kom de eerste afgeleide wel uit namelijk:

f'(x)= 2(x²-4x+5)/(2x-4)²

Maar de tweede afgeleide is fout bij mij en ik zou:

f''(x)= -1/(x-2)³.

Ik zou je m'n berekening wilen doorsturen maar het is veel te rommelig en volgens mij helemaal fout dus ik ga dat u niet aandoen. Zou je me willen helpen hoe ik aan de uitkomst kom?

Melike
29-10-2020

Antwoord

Hallo Melike,

Zeker bij toepassing van de quotiëntregel is het belangrijk om in kleine stapjes te werken, anders vliegen de vergissingen je om de oren. Van zowel de teller als de noemer heb je de afgeleide nodig. Handig is om vooraf een lijstje te maken van de teller (T), afgeleide van de teller (T'), noemer (N) en afgeleide van de noemer (N'):





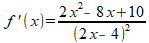
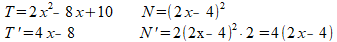
Nu heel zorgvuldig de quotiëntregel invullen:



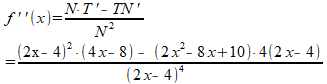
Teller en noemer delen door (2x-4):



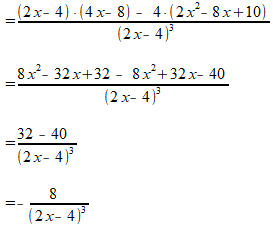
De laatste vorm is al best mooi, maar het kan nog wat mooier:



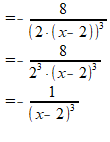
Schrijf de uitwerking zelf ook uit, alleen door ook zelf uit te werken ontwikkel je handigheid. Controleer of je steeds uitkomt op dezelfde tussenresultaten. Kijk goed welk soort vergissingen je (vaak) maakt, en probeer hier extra op te letten. Zo slijten vergissingen er wel uit.

GHvD
29-10-2020