WisFaq!

Drie mannen en drie vrouwen

Beste

Ik zit vast bij de volgende oefening:

Een vriendengroep bestaat uit zeven mannen en vijf vrouwen. Louis en Louise zijn het enige gehuwde koppel.

• Op hoeveel manieren kunnen hieruit drie mannen en drie vrouwen gekozen worden waarin het gehuwde koppel niet samen zit?

Aangezien herhaling niet mogelijk is en de volgorde niet van belang is, hebben we hier te maken met een combinatie. Ik zou op deze manier te werk gaan, maar deze klopt niet:

6C3(zonder Louis)·5C3 + 7C3·4C3(zonder Louise) + 6C3·4C3(zonder Louis en Louise)

Alvast bedankt!

Phybe
14-10-2020

Antwoord

Er zijn 4 mogelijke uitkomsten bij het kiezen van 3 mannen en 3 vrouwen uit een groep van mannen en vrouwen:

geen Louis - geen Louise
geen Louis - wel Louise
wel Louis - geen Louise
wel Louis - wel Louise

De laatste keus is niet toegestaan, maar de rest wel. Je berekening lijkt er wel op, maar 't klopt niet helemaal denk ik. Ik heb de volgende tekening gemaakt. De blauwe M en V's zijn de smurfen Louis en Louise...



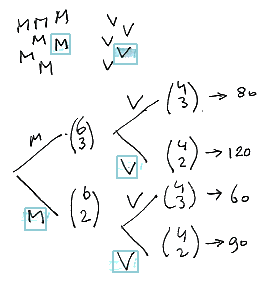
Gevalsonderscheiding en dan goed kijken wat je te kiezen hebt. Je moet maar kijken of je het kan volgen en of het klopt. Volgens mij kom je er dan wel uit.

WvR
14-10-2020