WisFaq!

Toegepaste differentiaalrekenen

De toegang tot een haven wordt aangegeven door twee bakens (N en S) die zich op een afstand A=500m van elkaar bevinden (zie tekening). De lijn tussen de bakens volgt de noord-zuid richting. Een schip vaart met een constante snelheid v in oostelijke richting, en bevindt zich op een afstand D=1200m van de lijn tussen de bakens. Baken N wordt op dat moment waargenomen onder een hoek θ=15°. De snelheid waarmee deze hoek op dat ogenblik verandert is 0.002 rad/s.

• Bepaal de snelheid waarmee het schip zich voortbeweegt. Bepaal ook de snelheid waarmee de afstand R tot baken S zal veranderen op het ogenblik dat het schip zich nog 500 meter van de grenslijn bevindt.

Zou iemand mij kunnen helpen aub?

Steeve
17-7-2020

Antwoord

Hallo Steeve,

Helaas zie ik geen tekening. Als ik de tekst goed begrijp, is dit de situatie:



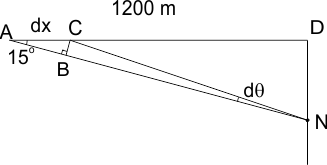
Het schip bevindt zich in punt A, onder een hoek θ=15° wordt het baken N waargenomen. de afstand AD is 1200 meter.

Als het schip verplaatst over een afstand dx, dan verandert de waarnemingshoek met dθ. In driehoek ABC geldt dan:

BC = AN·dθ
(eigenlijk: BC = BN·dθ, maar wanneer we dx laten naderen tot nul, dan vallen A en B samen).
dx = ^BC/_sin(15°)

dus:
dx = ^AN/_sin(15°)·dθ
^dx/_dt = ^AN/_sin(15°)·^dθ/_dt

Bereken dus de afstand AN, vul de gegeven hoeksnelheid in en je vindt de snelheid van het schip.

Voor jouw tweede vraag kan je een gelijksoortige schets maken.

GHvD
17-7-2020