WisFaq!

Normaalkromme

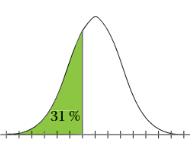
Als er om de normaalkromme een bepaalde oppervlakte is ingekleurd (percentage) hoe bereken je dan de ontbrekende grenzen? Ik dacht met Z-score maar gaat dit niet anders?

Timmy Van Epperzeel
14-6-2020

Antwoord

Dat hangt af van het gemiddelde en de standaardafwijking.

Voor de standaard normale verdeling met $
\mu = 0
$ en $
\sigma = 1
$ kan je met een tabel of rekenmachine de bijbenorende $z$-score bepalen:
$
z \approx {\rm{ - 0}}{\rm{,4959}}
$

Op De normale verdeling kan je zien het dan met mijn GR gaat.

Voor andere waarden van $
\mu
$ en $
\sigma
$ kan je bijbehorende grens berekenen. Gebruik daarvoor:

$
\eqalign{z = {{x - \mu } \over \sigma }}
$

Helpt dat?

---

Lesbrief normale verdeling
Van de 'oude' cursus statistiek 2-1 - 24 pagina's

---

WvR
14-6-2020