WisFaq!

Re: Gaten boren

Bij de productie van assen zijn de diameters X normaal verdeeld met N(gemiddelde= 12,64mm; standaardafwijking= 0,04mm)

Bij de geboorde gaten zijn de diameters Y eveneens normaal verdeeld met N(gemiddelde= 12, 70mm; standaardafwijking =0,03)

Vraag: We veronderstellen dat men bij het boren van de gaten het gemiddelde kan veranderen zonder dat de standaardafwijking verandert. Op welke gemiddelde diameter moet men de gaan boren opdat slechts 1% van de assen te dik zijn?
oplossing: ?
p(z$>$0)=0,01
P(z$>$(0-gemiddelde)/0;05)= 0,01
(0-gemiddelde)/0;05)= 2,33
gemiddelde= 11,65

Kavja
28-4-2020

Antwoord

Hallo Kavja,

Je komt een heel eind: alleen je laatste regel is onjuist, en de opgave is nog niet helemaal opgelost.

De laatste twee regels moeten zijn:
(0-gemiddelde)/0,05 = 2,33
0-gemiddelde = 0,1163 (niet tussentijds afronden en dan weer doorrekenen!)

gemiddelde = -0,1163

Om beter te begrijpen wat dit betekent, maak ik even een schets:



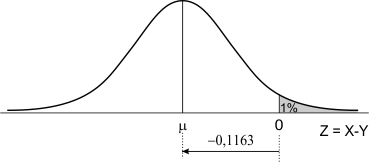
Je ziet dat het gemiddelde van Z, dus het gemiddelde verschil van de asdiameter en gatdiameter -0,1163 mm moet zijn om ervoor te zorgen dat slechts één procent van de assen niet in het gat past.
Je moet de gaten dus 0,1163 mm groter boren dan de gemiddelde diameter van de assen. De gemiddelde diameter van de gaten moet dus zijn:

Y_gem = 12,64 + 0,1163 = 12,76 mm

GHvD
28-4-2020