De functie $f$ bestaat alleen als $g(x)\gt0$, dus $-3\lt x \lt3$. Bovendien is $f(x)$ maximaal als $g(x)$ maximaal is en dat is dan bij $x=0$.
$f(x)=\log(9-0^2)=\log(9)$, dus het maximum van $g$ is $\log(9)$
Helpt dat?
WvR
25-9-2015
Als je van deze formule het bereik moet bepalen zonder rekenmachine lukt dit mij niet om dat dan geen max kunt zien.
f(x)=log(9-x2)
Hoe doe je dit dan?amasja
25-9-2015
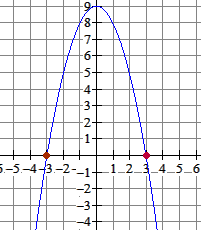
Als je naar $g(x)=-x^2+9$ kijkt dan ziet dat er zo uit:
De functie $f$ bestaat alleen als $g(x)\gt0$, dus $-3\lt x \lt3$. Bovendien is $f(x)$ maximaal als $g(x)$ maximaal is en dat is dan bij $x=0$.
$f(x)=\log(9-0^2)=\log(9)$, dus het maximum van $g$ is $\log(9)$
Helpt dat?
WvR
25-9-2015
#76384 - Functies en grafieken - Leerling bovenbouw havo-vwo