Jevraag is nog steeds niet helemaal duidelijk. Wat zijn a en b? En is de formule die je geeft de formule van het massatraagheidsmoment van een rechthoek? Dan zou het deze formule moeten zijn:
I = 1/12b∑a3
Ik vermoed dat je het volgende bedoelt, zie de figuur hieronder:
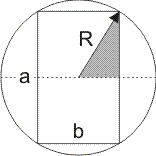
In een cirkel met straal R is een rechthoek getekend met zijden a en b. Bepaal de afmetingen van de rechthoek zodat het oppervlaktemoment ten opzichte van de as door het zwaartepunt evenwijdig aan b maximaal is.
Deze vraag kan je als volgt aanpakken:
In de grijze driehoek zie je:
(1/2a)2 + (1/2b)2 = R2
Hieruit kan je afleiden:
b = √(4R2-a2)
Vul deze uitrukking voor b in de formule van het traagheidsmoment. Gebruik wel de goede formule! Je krijgt een formule voor het traagheidsmoment waarin a de enige variabele is. Bepaal hiervan de afgeleide en stel deze gelijk aan nul. je vindt dan de waarde van a waarvoor het traagheidsmoment maximaal is.
GHvD
16-6-2015