WisFaq!

Een tovervierkant oplossen

In een magisch vierkant is de som van de getallen in elke rij en kolom en op de twee diagonalen telkens dezelfde. Welk getal moet dan op de plaats van het vraagteken in dit magisch vierkant komen? En hoe kom je hier aan?

15	21	...
...	...	...
12	...	?

Alexander
2-9-2014

Antwoord

Ik heb aan een aantal vakjes variabelen toegekend:



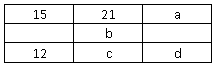
Je kunt dan 4 vergelijkingen opstellen met 4 onbekenden en dat oplossen:

12+a=2b
15+d=2b
12+d=21+b
21+c=2b

...en dan ben je er wel uit.

Ik zit nog wel te denken aan een 'intelligente' oplossing, maar dat zie ik nu even niet. Over de vergelijkingen moet je wel even nadenken, misschien...

naschrift
Ik zie nu dat je de eerste vergelijking eigenlijk niet nodig hebt. De laatste trouwens ook niet...

Dus met:
15+d=2b en 12+d=21+b ben je er al.

WvR
2-9-2014