WisFaq!

Bepalen van een rechte

Beste,
ik zit een beetje vast met een oefening,
zou u kunnen zeggen waar ik de fout in ga :

Dit is de opgave :
Bepaal een rechte l, evenwijdig met de x-as, die het gebied tussen y=-x²+9 en de x-as in twee gebieden verdeelt met dezelfde oppervlakte...

Ik heb mijn rechte l : y= p
- snijpunten gezocht : -x²+9 = p $\leftrightarrow$ x = √9-p
- integraal :
ondergrens = 0
bovengrens = √9-p
( p + x² - 9 )dx = 9
dit heb ik dan geïntegreerd ...
na veel vereenvoudiging kom ik uit bij
4/9p³+4p²- 28 p + 171 = 0
En vanaf hier zit ik volledig vast :(
Zou u mij kunnen helpen ?

Vriendelijke groeten
Paulien

Paulien
8-6-2014

Antwoord

Beste Paulien,

Laten we eens kijken naar de oorspronkelijke grafiek.


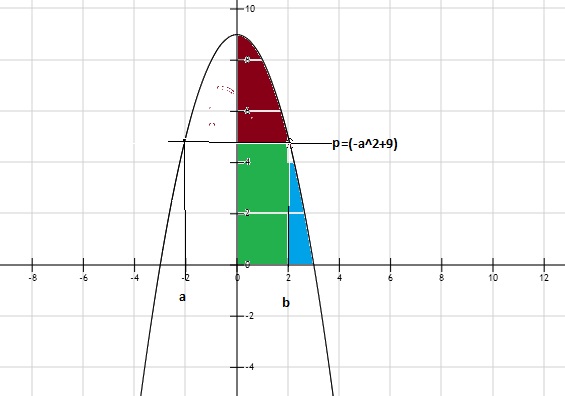
Je wilt een lijn y=p zodat het gebied boven en onder die lijn, ( ingesloten door x-as en de grafiek) hetzelfde is. Welnu het totale gebied is:

$
\int\limits_{ - 3}^3 { - x^2 + 9 = 36}
$

In de tekening wil je dus dat het door mij gearceerde gebied gelijk is aan 9.
Kortom het rode gebied wil je gelijk hebben aan 9.

rood+groen-groen=rood=9

rood+groen=
$ \int\limits_0^b { - x^2 + 9 = - \frac{1}{3}b^3 + 9b} $

groen is:
$
b( - b^2 + 9) = - b^3 + 9b
$

dus rood ( ofwel rood+groen-groen)=9
$
\begin{array}{l}
- \frac{1}{3}b^3 + 9b - ( - b^3 + 9b) = 9 \\
\frac{2}{3}b^3 = 9 \\
\end{array}
$

Ik neem aan dat je dan ook wel weet wat a is?

mvg DvL

DvL
8-6-2014