WisFaq!

Koordenvierhoek en gelijke afstanden

Gegeven een koordenvierhoek ABCD getekend in een gegeven cirkel C(O,r). De zijden AB en CD snijden elkaar in het punt P. Teken door P een evenwijdige p aan de diagonaal AC. De andere diagonaal BD snijdt dan de rechte p in het punt Q. Uit Q teken je de raaklijn QR aan de cirkel C(O,r) (raakunt is R en ik koos dat raakpunt links t.o.v. het punt Q). Toon dan aan dat de PQ = QR.

Mijn denkpiste: Het komt er op neer aan te tonen dat driehoek PQR gelijkbenig is. Ik verbond dan de punten P en R en het lijnstuk PR snijdt de cirkel in het punt S. Op zicht merkte ik meteen dat de bogen AS en SC gelijk leken te zijn, dus de hoeken op de corresponderende koorden zouden moeten gelijk zijn. Ik vond die hoeken wel, maar slaag er voorlopig niet in om effectief aan te tonen dat ze gelijk zijn.

Yves De Racker
7-11-2012

Antwoord

Hallo Yves,

Neem een andere 'piste'...
Zie onderstaande figuur; hierin is T (ipv R) het raakpunt van de raaklijn uit Q aan de cirkel.

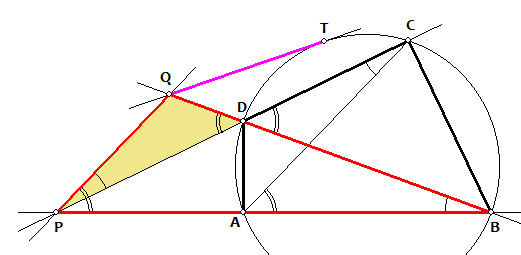
Je kan nu bewijzen dat:
--- QT² = QD × QB
geldend voor een raaklijnstuk aan een cirkel,
en ook via gelijkvormigheid van driehoeken - zie de gelijke hoeken - dat:
--- PQ² = QD × QB

Succes,
DK

dk
8-11-2012