WisFaq!

Binomiaal- en normale verdeling

Ik zit een beetje in de knoop met twee opgaven uit mijn cursus.

Eerste probleem:
In de lift van een gebouw met 10 verdiepingen stappen vier personen in op verdieping 0. Neem aan dat de kans dat een persoon op een gegeven verdieping uitstapt 1/10 is. Bereken de kans dat van de vier personen er twee samen op een verdieping uitstappen en de twee overigen samen op een andere verdieping.

Ik wou dit oplossen door drie groepen van personen te maken. De twee eerste groepen bevatten de personen die eerst uitstappen, en de derde groep worden de twee personen die samen op een andere verdieping uitstappen. Dan krijg je een binomiaalverdeling waarbij uitstappen van de eerste twee groepen als succes wordt gezien en het uitstappen van de derde groep als mislukking.

Dan zou je krijgen:
1) groep van twee uit vier: combinatie van twee uit drie: 4!/((4-2)!*2!) = 6
2) 3 groepen die uit de lift stappen:
(3
2) (1/10)² (9/10) = 27/1000
3) Vorige oplossing moet nog eens met factor 10 worden vermenigvuldigd omdat er tien verschillende verdiepingen zijn waar ze kunnen uitstappen. Dit geeft dus 27/100
4) Op deze manier zou de oplossing dus 27/100 * 6 = 1,62 moeten zijn, wat niet echt kan. Kan U me misschien vertellen wat ik verkeerd doe?

Probleem 2:
De hoeveelheid van een grondstof (uitgedrukt in tonnen), nodig gedurende een maand in een fabriek is een discrete stochastische variabele X. Uit ervaring, wat betreft de vraag naar het met deze grondstof vervaardigde product, heeft men:
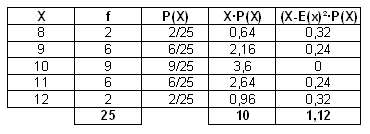
P(X8)=0 P(X=8)=2/25 P(X=9)=6/25 P(X=10)=9/25
P(X12)=0 P(X=12) =2/25 P(X=11) =6/25
Bereken E(X) en Var(X)

Oplossing:
Het gaat over een normale verdeling, dus E(X) = 10, maar hoe kan je hier Var(X) uithalen?

Iris
5-1-2003

Antwoord

Everything should be made as simple as possible, but not simpler.
Einstein, Albert (1879-1955)

1.
Op hoeveel manieren kunnen de mensen 2 aan 2 op dezelfde verdieping uitstappen en op hoeveel manieren kunnen 4 mensen de lift uitstappen. Je weet dan de kans.

Beschouw dit probleem als volgt: je hebt 10 bakjes en vier knikkers.

1. Op hoeveel manieren kun je 2 bakjes vullen met steeds 2 knikkers?
2. Op hoeveel manieren kan je 4 knikkers verdelen over 10 bakjes waarbij knikkers in meerdere bakjes mogen?

Als het goed is kan met elementaire combinatoriek wel uitkomen. Probeer het maar eens!

2.
Kort gezegd hebben we te maken met de volgende kansverdeling:

X	P(k=X)
8	2/25
9	6/25
10	9/25
11	6/25
12	2/25

Dit is geen normaal verdeling. Er staat zelfs bij dat het om een discrete verdeling gaat.

E(X)=8·²/₂₅+9·⁶/₂₅+...=10

Var(X)=(8-E(X))²·²/₂₅+(9-E(X))²·⁶/₂₅+...

Of anders gezegd:



..en zoals je ziet: geen binomiaal verdeling en geen normaal verdeling, maar gewoon 'zomaar' een kansverdeling. Gebruik de definities!

Hopelijk lukt het verder wel, anders horen we het wel.

WvR
6-1-2003