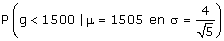WisFaq!

Normale verdeling met gegeven gemiddelde en standaarddeviatie

X: inhoud van een fles
X_gemeten = 1500 ml
X is normaal verdeeld met gemiddelde 1505 ml en een standaardafwijking van 4 ml.

Hoe groot is de kans dat de gemiddelde inhoud van een pakket van 5 flessen minder is dan 1500 ml.

Ik heb het zo proberen op te lossen:
P(1500 - a = X = 1500 + a)
normalcdf(ondergrens, bovengrens, E(x), sqr(Var(x))
normalcdf(1500 - 5, 1500 + 5, 1503, 4) = 49.70%

Is mijn redenering juist en zo niet wat is er dan verkeerd kan iemand de juiste oplossingswijze geven?

Met vriendelijke groet

Nathalieke
18-12-2008

Antwoord

Ik heb je vraag een beetje aangepast. In eerste instantie had ik niet helemaal begrepen wat je precies bedoelde. Ik denk dat 't antwoord nu wel klopt. Jouw redenering begrijp ik niet. Het gaat immers om de vraag 'wat is de kans dat het gemiddelde van 5 flessen kleiner is dan 1500', dus zal het dit moeten zijn:

X:inhoud van een fles
X~normaal verdeeld met m=1505 en s=4.
g=gemiddelde inhoud van een pakket van 5 flessen
Gevraagd:

Zie ook Wanneer moet je de wortel-n-wet gebruiken?

WvR
19-12-2008