1.
Met P:punten, Z:zijden en V:vlakken geldt voor een veelhoek in het platte vlak: P=n, Z=n en V=2, zodat geldt: P+V=Z+2
(V=2, omdat de figuur het platte vlak in 2 gebieden verdeelt)
Voorbeeld:
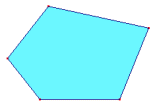
P=5
V=2
Z=5
5+2=5+2? Ja!
2.
Als we twee veelhoeken met een zijde aan elkaar plakken dan geldt:
(P1+P2-2)+3=(Z1+Z2-1)+2
(P1+P2)+5=(Z1+Z2)+3
(P1+P2)=(Z1+Z2)+2
Voorbeeld:
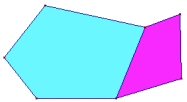
P1=5
Z1=5
V=3
P2=4
Z2=4
Z2=1
(5+4-2)+3=(5+4-1)+2?
7+3=8+2? Ja!
(3 vlakken? je kunt beter spreken over 3 gebieden... het blauwe, het paarse en het 'buitengebied')
3.
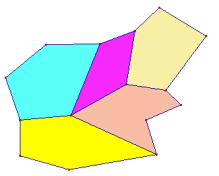
Met dit aan elkaar plakken van veelhoeken kan je door gaan. En steeds geldt: P+V=Z+2
4.
Het uitrekken of inkrimpen van zijden van de verschillende veelhoeken doet geen afbreuk aan de waarden van P, V en Z, zolang de lengte van een zijde maar geen nul wordt.
Je kunt zelfs alle veelhoeken weer onderverdelen in driehoeken, maar steeds blijft gelden: P+V=Z+2
5.
Een (convex) lichaam kan je op een speciale manier 'plat slaan' zodat je een plat figuur krijgt die ook voldoet aan P+A=Z+2. Die P's zijn de hoekpunten, die V's zijn het aantal vlakken en de Z's zijn de ribben. Dus geldt: H+V=R+2.
Voorbeeld:
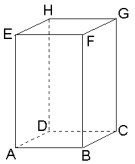
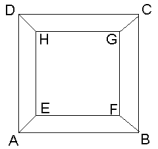
In de rechter figuur:
P=8
V=6
Z=12
8+6=12+2 klopt!
In de linker figuur:
H=8
V=6
R=12
8+6=12+2 klopt!
Zie Nineteen Proofs of Euler's Formula [http://www.ics.uci.edu/~eppstein/junkyard/euler/]
WvR
15-11-2001