WisFaq!

Normale verdeling

het aantal mannen dat in de zomermaanden per dag overlijdt aan een hartaanval is bij benadering normaal verdeeld met gemiddelde 27,6 en standaardafwijking 4,1

in figuur 3 zijn de 90%-grenzen van deze verdeling met stippellijnen aangegeven. dat betekent dat naar verwachting 90% van de staafjes een lengte heeft die tussen deze twee grenzen ligt. deze twee grenzen liggen symmetrisch ten opzichte van het gemiddelde. in figuur 3 is te zien dat de grenzen in de buurt van 20 en 35 liggen. met behulp van de hierboven genoemde normale benadering kun je deze twee grenzen nauwkeurig berekenen.

bereken deze twee grenzen in één decimaal nauwkeurig

ik snap dat je normalcdf(...) moet gebruiken, maar ik heb bepaalde cijfers geprobeerd en het klopt gewoon niet met het antwoord.

het antwoord
gebruik van de waarden 0,05 voor de linkergrens en 0,95 voor de rechtergrens. beschrijven hoe de GR kan worden gebruikt om de twee grenzen te berekenen. de linkergrens is 20,9. de rechtergrens is 34,3

een antwoord waar ik dus niets aan heb! wie o wie kan mij vertellen wat ik moet invoeren in mijn GR om dat antwoord te krijgen?

alvast super erg bedankt!

mariska
18-5-2008

Antwoord

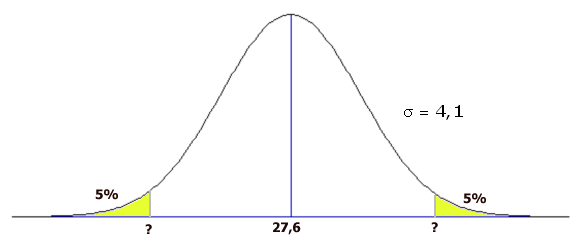
Met invNorm kan je bij een gegeven kans (de linker oppervlakte onder de grafiek), gemiddelde en standaarddeviatie 'terugrekenen'. Voor bijvoorbeeld de linkergrens tik je in:

| invNorm(0.05,27.6,4.1)

Afgerond geeft dit 20,9.

Omdat je alleen de kans (de oppervlakte onder de grafiek) onder een gegeven waarde kunt ingeven zal je voor de rechtergrens het volgende in moeten tikken:

| invNorm(0.95,27.6,4.1)

Vanwege de symmetrie is dat laatste niet 'echt' noodzakelijk. Uit het blote hoofd zou ik denken dat er 34,3 uitkomt...

Maar lukt dat verder zo?

Zie ook Met de grafische rekenmachine en Een soort overzicht.

WvR
18-5-2008