WisFaq!

Regressievergelijking

Ik stelde op 5-11-2002 de vragen over symmetrie en asymmetrie. Het is nog niet echt duidelijk.

Ik begrijp nog altijd niet echt goed waarom de regressielijn van Y gegeven X anders is als die van X gegeven Y. Komt dit dan door het feit dat je voorspellingen doet op basis van andere getallen en andere gemiddelden???

Met de standaardschattingsfout bedoel ik de gemiddelde fout die u maakt als u een schatting maakt met de regressielijn.

Mvg,
Ariane

Ariane
24-11-2002

Antwoord

Ik heb de punten (1,1),(2,2),(3,1) en (4,2)
Ik wil de regressielijn van Y gegeven X berekenen. Zo'n berekening kan je vinden op Kleinste kwadraten methode
Het blijkt Y=5X+1 te zijn. Als je dat tekent dan krijg je:



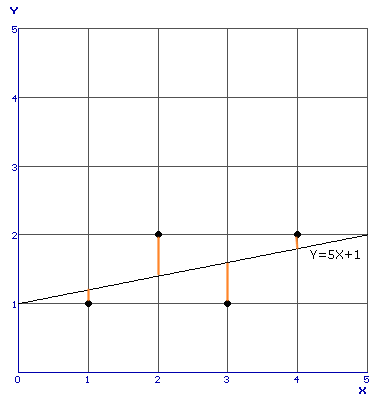
...hier in zijn de kwadraten van de afwijkingen (de rode lijnstukjes) het kleinst (zie Regressielijnen)

Bij de regressielijn X gegeven Y zou je de volgende situatie krijgen:



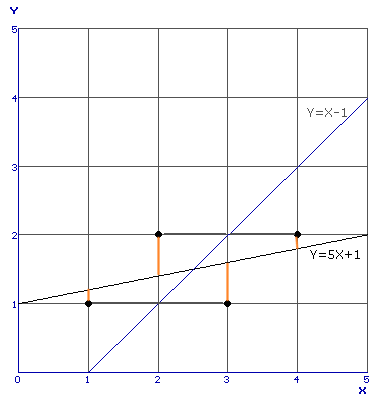
Nu moeten de kwadraten van de afwijkingen in verticale richting minimaal zijn en dat is duidelijk een hele andere situatie en levert dan ook een andere lijn en formule op.

Dit heeft alles te maken met variantie. Door de kwadraten van de afwijkingen te minimaliseren maak je de 'onverklaarde' variantie het kleinst.
Zie: Kleinste kwadraten methode

WvR
24-11-2002