WisFaq!

Vraagstuk afgeleiden

Gegeven f(x)=-x²+3. Bij de grafische voorstelling van deze functie zie je dat in het eerste kwadrant elk punt van de functie een rechthoek vormt met de oorsprong(0,0). Voor welke x- en y-waarde is de oppervlakte van deze rechthoek maximaal?

Zou u mij gewoon al een hint kunnen geven vanwaar af ik moet starten? En waarom vanaf daar? Ik dacht eerst de eerste afgeleide te berekenen:
f'(x)= -2x
Maar dan ben ik geen stap verder :-S

Alvast bedankt.

Stef
16-2-2008

Antwoord

Een tekening doet wonderen:



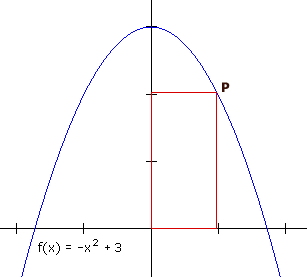
Druk vervolgens de oppervlakte van de rechthoek uit in x... en je hebt een functie voor de oppervlakte van de rechthoek als P over de parabool beweegt (met x tussen 0 en 3).

Met de afgeleide van die 'oppervlakte-functie' kan je dan de waarde voor 'x' berekenen waarvoor de oppervlakte maximaal is.

Nu jij weer...

Zie ook: 3. Optimaliseringsproblemen

WvR
16-2-2008